Probability with Measure
6.3 Jensen’s inequality \((\Delta )\)
A function \(g:\R \to \R \) is convex if it satisfies
\(\seteqnumber{0}{6.}{3}\)\begin{equation} \label {eq:convex_def} g(tx+(1-t)y)\leq tg(x)+(1-t)g(y) \end{equation}
for all \(x,y\in \R \) and \(t\in [0,1]\). Equation (6.4) is best understood with a picture.
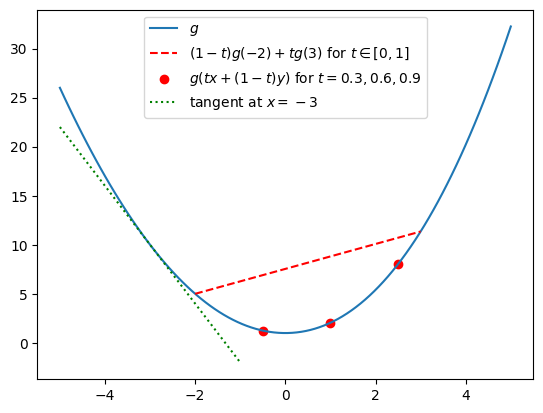
Convex functions are often described as having the shape of a smile. The key point is that the red dots, corresponding to the left hand side of (6.4), sit below the red line, corresponding to the right hand side of (6.4). Here we have shown (6.4) for \(x=-2\) and \(y=3\), on the convex function \(f(x)=1+x^2+\frac {1}{20}\max (0,x^3)\). The tangent line at \(-3\) is shown in green. Note that \(f\) sits above its own tangent lines.
Jensen’s inequality relates expectation with convex functions. It is a tool that requires a specific situation to apply, but when it does apply it is often the only tool available.
We will give a proof of Lemma 6.3.1 under the additional assumption that \(g\) is differentiable. This is not a very big restriction – in fact, convex functions are necessarily differentiable at all but countably many \(x\in \R \) (we won’t prove that). However, restricting to differentiable \(g\) allows us to give a much more intuitive proof than is possible in the general case. The following lemma explains why, and we’ll give the proof of Jensen’s inequality below. It says that a differentiable convex function sits above all of its tangent lines, as you can see in the example of the tangent at \(x=-3\) pictured in the graph above.
Proof: We’ll omit a proof of the first claim. It should help you understand (and check) convexity, but the proof doesn’t provide us with any useful intuition. In the picture below (6.4) you can see an example where \(g''(x)>0\) for all \(x\).
For the second claim, we can rewrite (6.4) as \((t+1-t)g(tx+(1-t)y) \leq tg(x)+(1-t)g(y)\), which rearranges to
\[t\l [g\big (tx+(1-t)y\big )-g(x)\r ] \leq (1-t)\l [g(y)-g\big (tx+(1-t)y\big )\r ].\]
Let us first consider when \(y>x\). In this case, for \(t\neq 1\), dividing through by \((1-t)(y-x)\) leads to
\(\seteqnumber{0}{6.}{4}\)\begin{equation} \label {eq:convex_tangents_0} t\frac {g\big (tx+(1-t)y\big )-g(x)}{(1-t)(y-x)} \leq \frac {g(y)-g\big (tx+(1-t)y\big )}{(1-t)(y-x)}. \end{equation}
The point is that \(tx+(1-t)y-x = (1-t)(y-x)\), so letting \(t\uparrow 1\) leads to
\(\seteqnumber{0}{6.}{5}\)\begin{equation} \label {eq:convex_tangents_1} g'(x)\leq \frac {g(y)-g(x)}{y-x}. \end{equation}
The result follows after multiplying both sides by \(y-x\).
When \(x<y\) the same calculation leads to the same result, but the direction of the inequality in (6.5) and (6.6) is reversed, then reverses back again when we multiply both sides by \(y-x\). The case \(x=y\) is trivial. ∎
Proof of Lemma 6.3.1 for differentiable \(g\): By part 2 of Lemma 6.3.2 we have \((y-x)g'(x)\leq g(y)-g(x)\) for all \(x,y\in \R \). Therefore we may put \(\E [X]\) in place of \(x\) and \(X\) in place of \(y\), leading to
\[(X-\E [X])g'(\E [X])\leq g(X)-g(\E [X]).\]
Taking expectations, using linearity and monotonicity,
\(\seteqnumber{0}{6.}{6}\)\begin{align*} (\E [X]-\E [X])g'(\E [X])\leq \E [g(X)]-g(\E [X]). \end{align*} The left hand side is zero, and the result follows. ∎
-
Example 6.3.3 Setting \(g(x)=x^2\) in Jensen’s inequality gives \(\E [X]^2\leq \E [X^2]\). We derived this inequality already in Exercise 5.12 as a consequence of the Cauchy-Schwarz inequality. Setting \(g(x)=|x|^p\) for \(p\geq 1\) gives that \(\E [|X|^p]\leq \E [|X|]^p\), which we will make use of in the proof of Lemma 7.2.1. Note that for \(p\in [1,2)\), the function \(x\mapsto |x|^p\) is convex but is not differentiable at \(x=0\).
-
Remark 6.3.4 Jensen’s inequality also holds if the convex function \(g\) is only defined on some interval \(I\) of \(\R \), but \(I\) is large enough that \(\P [X\in I]=1\). The proof is the same as above, except that the first inequality in the proof only holds almost surely. Lemma 6.3.2 still holds, but with \(x\) and \(y\) restricted to \(I\).
Jensen’s inequality is surprisingly far reaching in its consequences. For example it provides the key ingredient used to prove most of the basic inequalities of functional analysis e.g. Hölders inequality, Minkowski’s inequality, Young’s inequality, and so on. The road towards those inequalities is fairly long and begins with Exercise 6.5, but we won’t include those inequalities in this course.