Probability with Measure

2.2 Liminf and limsup

The main difficulty with limits is that, in general, limits do not exist. Most sequences do not converge to anything. However there are two closely related concepts that always exist. They are much easier to work with but they take more care to define.

Let $(a_{n})$ be a sequence of real numbers. Note that the sequence $b_{n} = sup_{k \geq n} a_{k}$ is monotone decreasing, because as $n$ gets larger the set ${a_{k}; k \geq n}$ contains less terms. Lemma 2.1.1 implies that this sequence has a limit, with the caveat that the limit might be infinite. The sequence $(b_{n})$ is monotone decreasing, so its limit is equal to $inf_{n \in N} b_{n}$ . With this is mind we make the following definition:

$\begin{matrix} (2.3) & \underset{n \to \infty}{lim sup} a_{n} = lim_{n \to \infty} (sup_{k \geq n} a_{k}) = inf_{n \in N} (sup_{k \geq n} a_{k}) . \end{matrix}$

Heuristically, $\underset{n}{lim sup} a_{n}$ is the smallest value that the tail of the sequence $(a_{n})$ stays below.

We can do the same construction the other way up, which gives

$\begin{matrix} (2.4) & \underset{n \to \infty}{lim inf} a_{n} = lim_{n \to \infty} (inf_{k \geq n} a_{k}) = sup_{n \in N} (inf_{k \geq n} a_{k}) . \end{matrix}$

Heuristically, $\underset{n}{lim inf} a_{n}$ is the largest value that the tail of the sequence $(a_{n})$ stays above. Note that (2.3) and (2.4) are always well defined, as extended real numbers, and that $\underset{n}{lim inf} a_{n} \leq \underset{n}{lim sup} a_{n}$ .

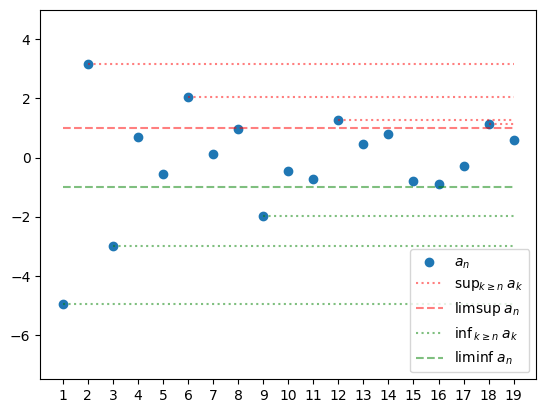
Example 2.2.1 It is helpful to see a picture:

The sequence displayed is a sample of $a_{n} = \cos (n) + 10 \frac{(- 1)^{n}}{n} U_{n}$ , where $(U_{n})$ are i.i.d. uniform random variables on $[0, 1]$ . This is chosen to make a clear picture. As $n \to \infty$ the $\cos (n)$ term will oscillate within $[- 1, 1]$ and the second term will tend to zero. Note that the dotted lines converge downwards to $\underset{n}{lim sup} a_{n} = 1$ (in red) and upwards to $\underset{n}{lim inf} a_{n} = - 1$ (in green).

We will spend the rest of this section making connections between $lim inf$ , $lim sup$ and $lim$ .

Lemma 2.2.2 Let $(a_{n})$ be a sequence of extended reals. Then:
- 1. The sequence $(a_{n})$ converges if and only if $\underset{n \to \infty}{lim inf} a_{n} = \underset{n \to \infty}{lim sup} a_{n}$ .
- 2. If $(a_{n})$ converges then $\underset{n \to \infty}{lim inf} a_{n} = \underset{n \to \infty}{lim sup} a_{n} = lim_{n \to \infty} a_{n}$ .

Proof: Suppose first that $(a_{n})$ converges, say $a_{n} \to a$ . We will consider the case $a \in R$ here; the case $a = \pm \infty$ is similar and we will omit it, as discussed in Remark 2.1.2. For all $ϵ > 0$ there exists $n \in N$ such that $| a_{k} - a | \leq ϵ$ for all $k \geq n$ . Hence $a - ϵ \leq a_{k} \leq a + ϵ$ for all $k \geq n$ , which implies that

$a - ϵ \leq inf_{k \geq n} a_{k} \leq sup_{k \geq n} a_{k} \leq a + ϵ$

Without loss of generality we may choose $n \geq \frac{1}{ϵ}$ . Letting $ϵ \to 0$ , upon which $n \to \infty$ , gives that

$a = \underset{n}{lim inf} a_{n} = \underset{n}{lim sup} a_{n} .$

We have therefore proved both part 2 and the forwards implication of part 1.

We need to prove the reverse implication from part 1. Suppose that $\underset{n}{lim inf} a_{n} = \underset{n}{lim sup} a_{n} \in R$ (and we don’t yet know that $(a_{n})$ converges). For all $n \in N$ we have

$\begin{matrix} (2.5) & 0 \leq a_{n} - inf_{k \geq n} a_{k} \leq sup_{k \geq n} a_{k} - inf_{k \geq n} a_{k} . \end{matrix}$

Note also that

$\begin{matrix} (2.6) & lim_{n \to \infty} (sup_{k \geq n} a_{k} - inf_{k \geq n} a_{k}) = \underset{n \to \infty}{lim sup} a_{n} - \underset{n \to \infty}{lim inf} a_{n} = 0. \end{matrix}$

Combining (2.5) with (2.6) and using the sandwich rule, we have

$\begin{matrix} (2.7) & lim_{n \to \infty} (a_{n} - inf_{k \geq n} a_{k}) = 0. \end{matrix}$

We can write $a_{n} = (a_{n} - inf_{k \geq n} a_{k}) + inf_{k \geq n} a_{k}$ , and we know that both of these terms have a limit as $n \to \infty$ . The first tends to zero by (2.7) and the second converges to $\underset{n}{lim inf} a_{n}$ . From the algebra of limits we thus obtain that $(a_{n})$ converges and $lim_{n} a_{n} = \underset{n}{lim inf} a_{n}$ . Since $\underset{n}{lim inf} a_{n} = \underset{n}{lim sup} a_{n}$ was our assumption, this completes the proof. ∎

Lemma 2.2.3 Let $(a_{n})$ be a sequence of extended reals. Then $\underset{n}{lim sup} (- a_{n}) = - \underset{n}{lim inf} a_{n}$ .

Proof: You already know from real analysis that $sup_{n} (- a_{n}) = - inf_{n} a_{n}$ for real $a_{n}$ . This equation also holds for extended reals, but we’ll omit checking the extra cases involving infinities here. The result follows from this along with (2.3) for $lim sup$ , and with (2.4) for $lim inf$ . ∎