Probability with Measure

4.5 The Lebesgue integral

At last we are ready for the final step in the construction of the Lebesgue integral, which extends our current framework to a class of measurable functions that are real-valued, instead of just non-negative. This step requires a little preparation. We continue to work over an arbitrary measure space \((S,\Sigma ,m)\).

For a function \(f:S\to \R \) we define

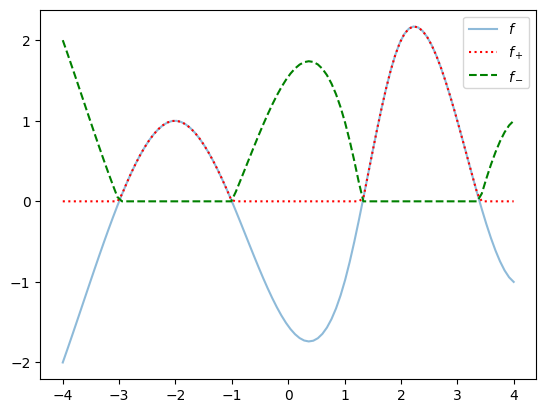
\[f_+=\max (f,0), \qquad f_-=\max (-f,0),\]

which are pointwise definitions of functions \(f_+,f_-:S\to \R \). It is easiest to see what is going on here with a picture:

Note that

\[f=f_+-f_-,\]

and that by Theorem 3.1.5 both \(f_+\) and \(f_-\) are non-negative measurable functions from \(S\) to \(\R \). Step 2 (Definition 4.2.1) tells us the values of \(\int _S f_+\,dm\) and \(\int _S f_-\,dm\), which are extended real numbers in \([0,\infty ]\). Note also that \(|f|=f_++f_-\), and that \(\int _S |f|\,dm\) is also covered by Step 2.

Definition 4.5.1 (Lebesgue Integral, Step 3) Let \(f:S\to \R \) be measurable. If at least one of \(\int _S f_+\,dm\) and \(\int _S f_-\,dm\) is not equal to \(+\infty \), then we define
\(\seteqnumber{0}{4.}{14}\)
\begin{equation} \label {eq:leb_int_full} \int _S f\,dm = \int _S f_+\,dm-\int _S f_- \,dm, \end{equation}

which is an extended real number.

If both \(\int _S f_+\,dm\) and \(\int _S f_-\,dm\) are equal to \(+\infty \) then \(\int _S f\,dm\) is undefined. Note that in this case (4.15) would give \(\infty -\infty \), which is undefined.

It is important that we have a way to avoid handling infinities. This is provided by the following definition:

For non-negative measurable functions part 1 is contained within Theorem 4.4.1. Thus \(\int _A f_{\pm }\,dm + \int _B f_{\pm }\,dm = \int _{A\cup B}f_{\pm }\,dm\). Subtracting the \(f_-\) case from the \(f_+\) case gives

\[\int _A f_+\,dm - \int _A f_-\,dm + \int _B f_+\,dm - \int _B f_-\,dm = \int _{A\cup B}f_+\,dm - \int _{A\cup B}f_-\,dm\]

which by (4.15) is exactly what we need to prove part 1.

For parts 2-5, it suffices to prove the case \(S=A\). Note that in view of Definition 4.1.3 we can recover the general case by replacing \(f\) and \(g\) by \(\1_A f\) and \(\1_A g\). Part 5 follows immediately from Lemma 4.2.6 and (4.15). Several of the remaining parts are left for you as excerises. Part 3 is Exercise 4.4 part (c). Part 4 is Exercise 4.4 part (a). For part 2, Exercise 4.4 part (d) shows that

\begin{equation} \label {eq:leb_int_step_3_lin_part_1} \alpha \int _S f\,dm = \int _S \alpha f\,dm \end{equation}

for all \(f\in \Lone \). In order to prove part 2 it remains only to show that

\begin{equation} \label {eq:leb_int_step_3_lin_part_2} \int _S f+g\,dm = \int _S f\,dm + \int _S g\,dm. \end{equation}

We will prove (4.18) here. Note that we may assume that both \(f, g\) are not identically \(0\), because \(\int _S 0\,dm=0\). The fact that \(f+g\) is in \(\Lone \) if \(f\) and \(g\) are follows from Exercise 4.4 part (b).

To show (4.18) we first need to consider six different special cases. Writing \(h=f+g\), these cases are (1) \(f \geq 0, g \geq 0, h \geq 0\), (2) \(f \leq 0, g \leq 0, h \leq 0\), (3) \(f \geq 0, g \leq 0, h \geq 0\), (4) \(f \leq 0, g \geq 0, h \geq 0\), (5) \(f \geq 0, g \leq 0, h \leq 0\), (6) \(f \leq 0, g \geq 0, h \leq 0\). Note that case (1) is precisely Lemma 4.3.2. We’ll just prove case (3) here, and note that the others are similar. To show case (3) we write \(f = h + (-g)\) and, noting that all these are non-negative functions, from Lemma 4.3.2 we obtain \(\int _{S}f\, dm = \int _{S}(f+g)\, dm + \int _{S}(-g)\,dm\), and hence from (4.17) we have \(\int _{S}(f+g)\, dm = \int _{S}f \,dm - \int _{S}(-g)\,dm = \int _{S}f \,dm + \int _{S}g\,dm,\) which proves case (3).

For a general \(f\in \Lone \), we write \(S = S_{1} \cup S_{2} \cup S_{3} \cup S_{4} \cup S_{5} \cup S_{6}\), where \(S_{l}\) is the set of all \(x \in S\) for which case (\(l\)) holds for \(l=1,2, \ldots , 6\). These sets are disjoint and measurable. We then have

\[ \int _{S}(f + g)\,dm = \sum _{i=1}^{6}\int _{S_{i}}(f + g) \,dm = \sum _{i=1}^{6}\int _{S_{i}}f \,dm + \sum _{i=1}^{6}\int _{S_{i}}g\, dm = \int _{S}f\,dm + \int _{S}g \,dm.\]

In the above, the first and last equalities use part 1 of the present lemma, and the middle equality uses cases (1)-(6) above. This completes the proof of part 2. ∎