Stochastic Processes and Financial Mathematics
(part two)
Chapter 19 Financial networks \(\msconly \)
Following the financial crisis of 2007/08, both regulators and banks have become more interested in viewing the financial system as a connected whole – as opposed to viewing it as a collection of isolated institutions. With this new perspective, one aspect that commands special attention is debt contagion.
Debt contagion refers to the following scenario. Consider a connected network of banks who lend to each other. Suppose that one of these institutions, call it bank A, suddenly fails (i.e. goes bankrupt) and is then unable to pay its debts. In doing so, A harms its neighbours (i.e. banks who lent to A). Some of the neighbours of A may then also fail, and be unable to pay their own debts, harming their own neighbours – and so on. This process is usually known as a cascade. Potentially, the end result could be that a large fraction of the whole network fails.
As we discussed in Chapter 18, it is known that the global financial system was at risk of precisely this scenario during parts of the financial crisis of 2008. Since then, there has been effort within the mathematical finance research community to provide models that describe when, and precisely how, such a risk is felt. In this section we give a brief introduction to one of the first (and consequently, simplest) models that was developed, followed by a discussion of how it was later extended.
19.1 Graphs and random graphs \(\msconly \)
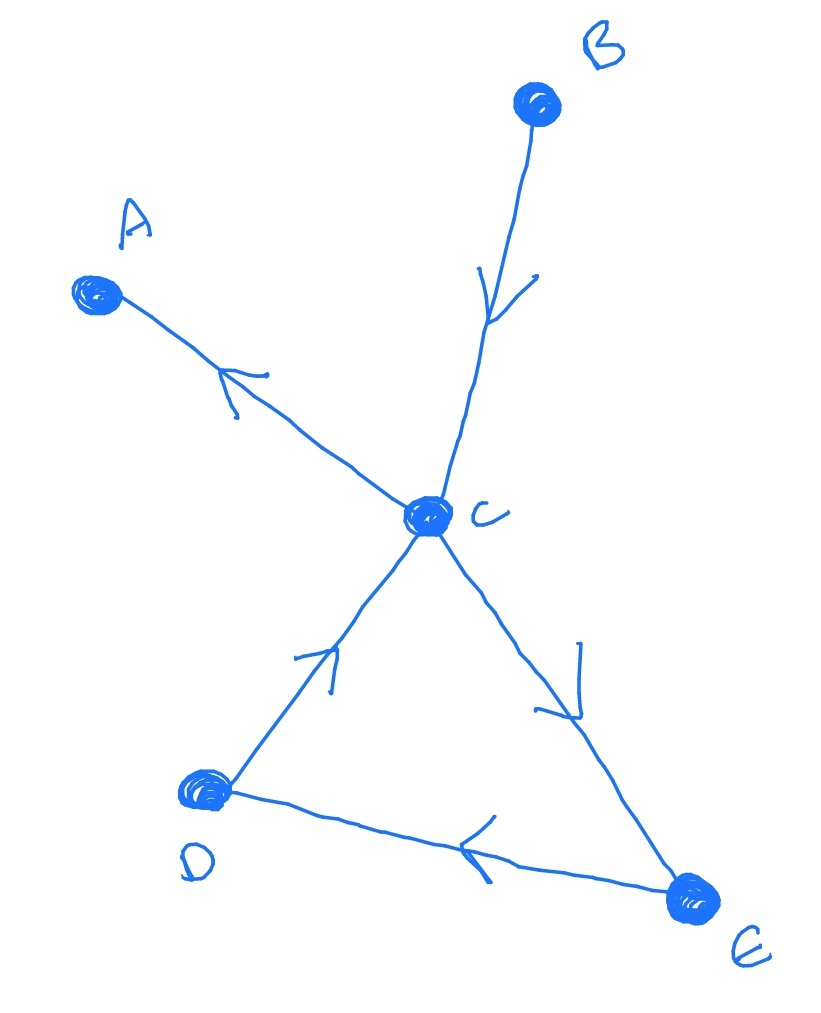
A network is a set of nodes, some of which are connected together by edges. For example,
Here, the nodes are \(A,B,C,D,E\). The terms graph and network are usually used interchangeably. The terms vertex and node are also used interchangeably. We’ll use all these terms.
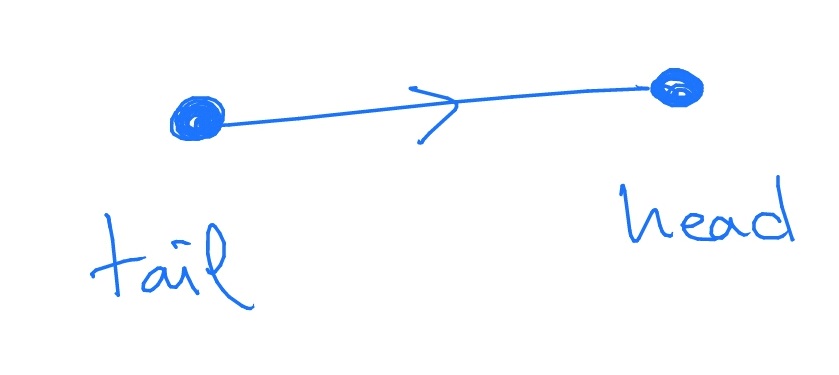
We will always be interested in the directed case, in which each edge has a direction. In the graph above this direction is signified by the direction of the arrows. The node at the start of an edge is called the head (of the edge) and the node at the end of the edge is called the tail (of the edge).
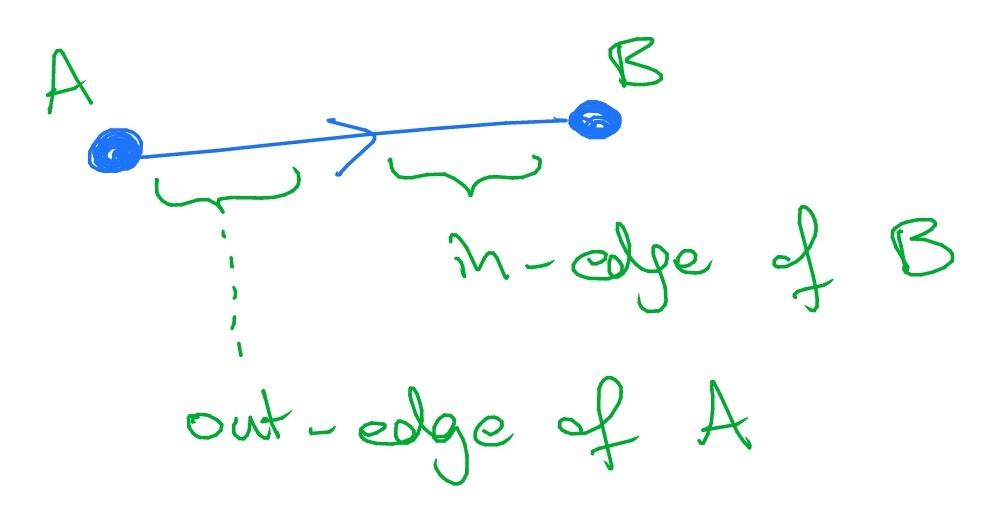
We write \(\indeg (i)\) for the number of edges that have node \(i\) as their head, and we call each such edge an in-edge of \(i\). We write \(\outdeg (i)\) for the number of edges that have \(i\) as their tail, and we call each such edge an out-edge of \(i\). It’s common to imagine each edge as split in half, with an ‘in’ part and an ‘out’ part
We write an edge as \((\text {tail},\text {head})\). So the edge of the graph above are \((C,A)\), \((B,C)\), \((C,E)\), \((E,D)\) and \((D,C)\).
Formally, a graph is a pair \(G=(V,E)\) where \(V\) is the set of vertices and \(E\) is a set of ordered pairs of vertices. Each element of \(E\) has the form \((v_1,v_2)\), where \(v_1,v_2\in V\), and denotes an edge with source \(v_1\) and sink \(v_2\). In this notation, our graph is
\[G=(V,E)\text { where }V=\{A,B,C,D,E\}\text { and }E=\{(C,A), (B,C), (C,E), (E,D), (D,C)\}.\]
Given a graph \(G=(V,E)\), the degree distribution of \(G\) is the distribution of the random variable
\(\seteqnumber{0}{19.}{0}\)\begin{equation} \label {eq:deg_dist} D_G=(\indeg (v),\outdeg (v)), \end{equation}
where \(v\) is a node sampled uniformly at random from \(V\). In words, \(D_G\) is the (bivariate) random variable who’s distribution matches the frequencies of in/out degrees present in nodes of \(G\). For example, for the graph above we have \(5\) nodes and
\[ \begin {alignedat}{2} \P [D_G=(1,0)]&=\frac 15\hspace {5pc}&&\text {(node $A$)}\\ \P [D_G=(0,1)]&=\frac 15&&\text {(node $B$)}\\ \P [D_G=(2,2)]&=\frac 15&&\text {(node $C$)}\\ \P [D_G=(1,1)]&=\frac 25&&\text {(nodes $D$ and $E$)}\\ \end {alignedat} \]
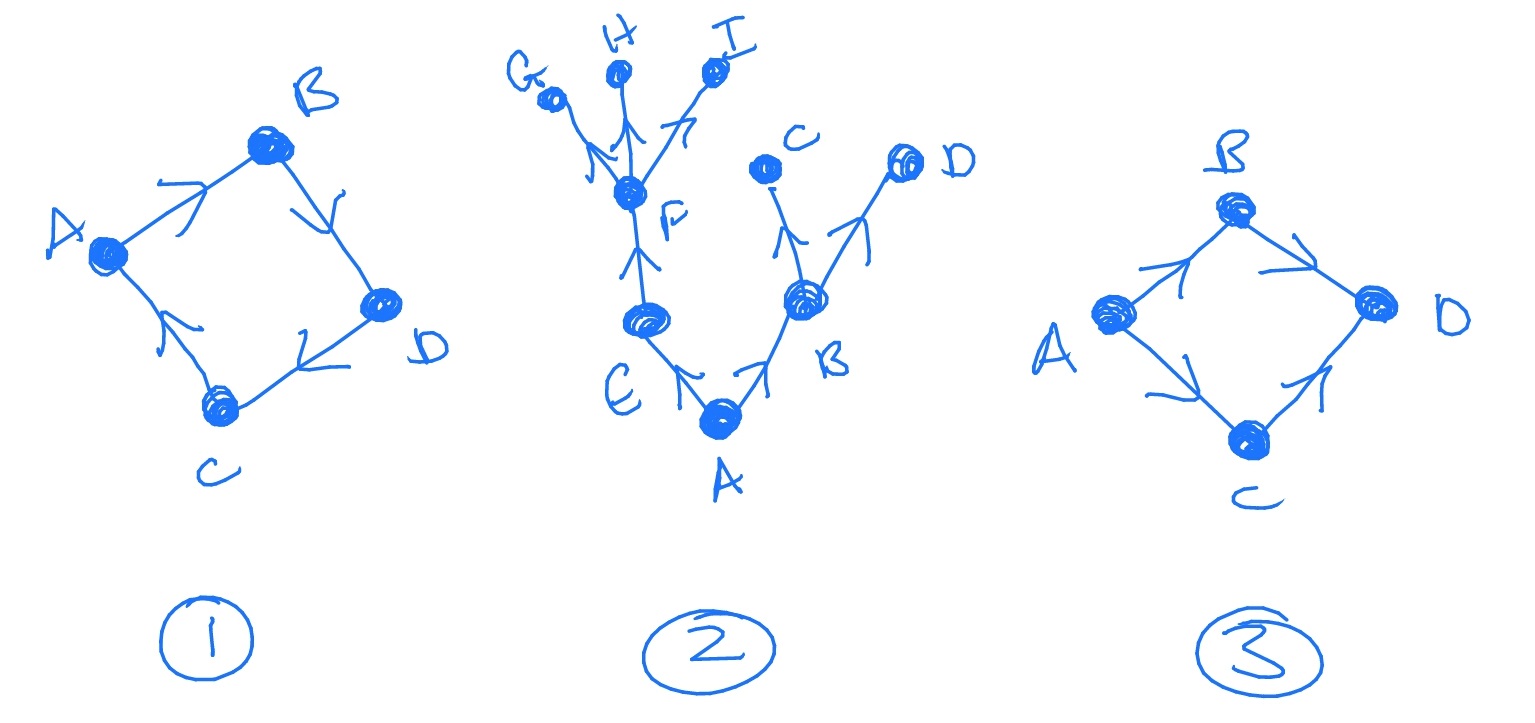
A random graph is, as you might expect, a graph where the sets of edges and vertices are both randomly sampled. We’ll come back to thinking about random graphs in Section 19.3. A graph is said to be a tree if, between any pair \(A,B\) of vertices, there is precisely one path along edges (travelling in the direction they point) that gets from \(A\) to \(B\). It is perhaps clearest from a picture:
Graph 1 is not a tree: for example, to get from \(A\) to \(A\) we can take the paths \(ABDCA\) and \(ABDCABDCA\). Graph 2 is a tree, because for any pair of vertices there is only one way to get between them. Graph 3 is not a tree: for example to get from \(A\) to \(D\) we can take the paths \(ABD\) and \(ACD\).