Stochastic Processes and Financial Mathematics
(part two)

Chapter C Solutions to exercises (part two)

Chapter 11

• 11.1

  • (a) We have \(C_t=\mu t+\sigma B_t\). Hence,

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \E [C_t]&=\E [\mu t + \sigma B_t]=\mu t+\sigma \E [B_t]=\mu t\\ \E [C_t^2]&=\E [\mu ^2t^t+2t\mu \sigma B_t+\sigma ^2 B_t^2]=\mu ^2t^2+2t\mu \sigma (0)+\sigma ^2t=\mu ^2t^2+\sigma ^2t\\ \var (C_t)&=\E [C_t^2]-\E [C_t]^2=\sigma ^2 t. \end{align*} where we use that \(\E [B_t]=0\) and \(\E [B_t^2]=t\).

  • (b) We have

    \[C_t-C_u=\mu t+ \sigma B_t-\mu u-\sigma B_u=\mu (t-u)+\sigma (B_t-B_u)\sim \mu (t-u)+\sigma N(0,t-u)\]

    where, in the final step, we use the definition of Brownian motion. Then, by the scaling properties normal random variables we have \(C_t-C_u\sim N(\mu (t-u), \sigma ^2(t-u))\).

  • (c) Yes. By definition, Brownian motion \(B_t\) is a continuous stochastic process, meaning that the probability that \(B_t\) is a continuous function is one. Since \(t\mapsto \mu t\) is a continuous function, we have that \(\mu t+\sigma B_t\) is a continuous function with probability one; that is, \(B_t\) is a continuous stochastic process.

  • (d) We have \(\E [C_t]=\mu t\), but Brownian motion has expectation zero, so \(C_t\) is not a Brownian motion.

• 11.2 We have

  \(\seteqnumber{0}{C.}{0}\)

  \begin{align*} \cov (B_u,B_t)&=\E [B_tB_u]-\E [B_t]\E [B_u]\\ &=\E [B_tB_u]\\ &=\E [(B_t-B_u)B_u]+\E [B_u^2]\\ &=\E [B_t-B_u]\E [B_u]+\E [B_u^2]\\ &=0\times 0 +u\\ &=u \end{align*} Here, to deduce the fourth line, we use the second property in Theorem 11.2.1, which tells us that \(B_t-B_u\) and \(B_u\) are independent.

• 11.3 When \(u\leq t\) the martingale property of Brownian motion (Lemma 11.4.3) implies that \(\E [B_t\|\mc {F}_u]=B_u\). When \(t\leq u\) we have \(B_t\in \mc {F}_u\) so by taking out what is known we have \(\E [B_t\|\mc {F}_u]=B_t\). Combing the two cases, for all \(u\geq 0\) and \(t\geq 0\) we have \(\E [B_t\|\mc {F}_u]=B_{\min (u,t)}\).

• 11.4

  • (a) We’ll use the pdf of the normal distribution to write \(\E [B_t^n]\) as an integral. Then, integrating by parts (note that \(\frac {d}{dz}e^{-\frac {z^2}{2t}}=\frac {-z}{t}e^{-\frac {z^2}{2t}}\)) we have

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \E [B_t^n] &=\frac {1}{\sqrt {2\pi t}}\int _{-\infty }^\infty z^n e^{-\frac {z^2}{2t}}\,dz\\ &=\frac {1}{\sqrt {2\pi t}}\int _{-\infty }^\infty \l (-t z^{n-1}\r )\l (\frac {-z}{t} e^{-\frac {z^2}{2t}}\r )\,dz\\ &=\l [-\frac {1}{\sqrt {2\pi t}}tz^{n-1}e^{-\frac {z^2}{2t}}\r ]_{z=-\infty }^\infty +\frac {1}{\sqrt {2\pi t}}\int _{-\infty }^\infty t(n-1)z^{n-2}t e^{-\frac {z^2}{2t}}\,dz\\ &=0+t(n-1)\E [B_t^{n-2}]. \end{align*}

  • (b) We use the formula we deduced in part (a). Since \(\E [B_t^0]=\E [1]=1\), we have \(\E [B_t^2]=t(2-1)(1)=t\). Hence \(\E [B_t^4]=t(4-1)\E [B_t^2]=t(4-1)t=3t^2\) and therefore \(\var (B_t^2)=\E [B_t^4]-\E [B_t^2]^2=2t^2\).

  • (c) Again, we use the formula we deduced in part (a). Since \(\E [B_t]=0\) it follows (by a trivial induction) that \(\E [B_t^n]=0\) for all odd \(n\in \N \). For even \(n\in \N \) we have \(\E [B_t^2]=t\) and (by induction) we obtain

    \[\E [B_t^n]=t^{n/2} (n-1)(n-3)\ldots (1).\]

  • (d) We have \(\var (B_t^n)=\E [B_t^{2n}]-\E [B_t^n]^2\) which is finite by part (c). Hence \(B_t^n\in L^2\), which implies that \(B_t^n\in L^1\).

• 11.5 Using the scaling properties of normal random variables, we write \(Z=\mu +Y\) where \(Y\sim N(0,\sigma ^2)\). Then, \(e^Z=e^\mu e^Y\) and

  \(\seteqnumber{0}{C.}{0}\)

  \begin{align*} \E [e^Y] &=\frac {1}{\sqrt {2\pi }\sigma }\int _{-\infty }^\infty e^y e^{-\frac {y^2}{2\sigma ^2}}\,dy\\ &=\frac {1}{\sqrt {2\pi }\sigma }\int _{-\infty }^\infty \exp \l \{-\frac {1}{2\sigma ^2}\l (y^2-2\sigma ^2y\r )\r \}\,dy\\ &=\frac {1}{\sqrt {2\pi }\sigma }\int _{-\infty }^\infty \exp \l \{-\frac {1}{2\sigma ^2}\l ((y-\sigma ^2)^2-\sigma ^4\r )\r \}\,dy\\ &=e^{\frac {\sigma ^2}{2}}\frac {1}{\sqrt {2\pi }\sigma }\int _{-\infty }^\infty \exp \l \{-\frac {(y-\sigma ^2)^2}{2\sigma ^2}\r \}\,dy\\ &=e^{\frac {\sigma ^2}{2}}. \end{align*} Here, to deduce the third line we complete the square, and to deduce the final line we use that the p.d.f. of a \(N(\sigma ^2,\sigma )\) random variable integrates to \(1\). Therefore,

  \[\E [e^Z]=e^\mu \E [e^Y]=e^{\mu +\frac {\sigma ^2}{2}}.\]

• 11.6

  • (a) Since \(B_t\) is adapted, \(e^{\sigma B_t-\frac 12\sigma ^2 t}\) is also adapted. By (11.2) and scaling of normal random variables we have that \(e^{\sigma B_t-\frac 12\sigma ^2 t}\) is in \(L^1\). It remains only to check that

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \E \l [\exp \l (\sigma B_t-\frac 12\sigma ^2 t\r )\|\mc {F}_u\r ] &=\E \l [\exp \l (\sigma (B_t-B_u)+\sigma B_u-\frac 12\sigma ^2 t\r )\|\mc {F}_u\r ]\\ &=\exp \l (\sigma B_u-\frac 12\sigma ^2 t\r )\E \l [\exp \l (\sigma (B_t-B_u)\r )\|\mc {F}_u\r ]\\ &=\exp \l (\sigma B_u-\frac 12\sigma ^2 t\r )\E \l [\exp \l (\sigma (B_t-B_u)\r )\r ]\\ &=\exp \l (\sigma B_u-\frac 12\sigma ^2 t\r )\exp \l (\frac 12\sigma ^2(t-u)\r )\\ &=\exp \l (\sigma B_u-\frac 12\sigma ^2u\r ). \end{align*} Here, the second line follows by taking out what is known, since \(B_u\) is \(\mc {F}_u\) measurable. The third line then follows by the definition of Brownian motion, in particular that \(B_t-B_u\) is independent of \(\mc {F}_u\). The fourth line follows by (11.2), since \(B_t-B_u\sim N(0,t-u)\) and hence \(\sigma (B_t-B_u)\sim N(0,\sigma ^2(t-u))\).

  • (b) Since \(B_t\) is adapted, \(B_t^3-3tB_t\) is also adapted. From 11.4 we have \(B_t^3,B_t\in L^1\), so also \(B_t^3-tB_t\in L^1\). Using that \(B_u\) is \(\mc {F}_u\) measurable, we have

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \E \l [B_t^3-3tB_t\|\mc {F}_u\r ] &=\E \l [(B_u^3-3uB_u)+B_t^3-3tB_t-(B_u^3-3uB_u)\|\mc {F}_u\r ] \\ &=B_u^3-3uB_u+\E \l [B_t^3-B_u^3-3tB_t+3uB_u\|\mc {F}_u\r ] \end{align*} so we need only check that the second term on the right hand side is zero. To see this,

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \E \l [B_t^3-B_u^3-3tB_t+3uB_u\|\mc {F}_u\r ] &=\E \l [B_t^3-B_u^3-3tB_u+3uB_u-3t(B_t-B_u)\|\mc {F}_u\r ]\\ &=\E \l [B_t^3-B_u^3-3tB_u+3uB_u\|\mc {F}_u\r ]+0\\ &=\E \l [B_t^3-B_u^3\|\mc {F}_u\r ]-3B_u(t-u)\\ &=\E \l [(B_t-B_u)^3+3B_t^2B_u-3B_u^2B_t\|\mc {F}_u\r ]-3B_u(t-u)\\ &=\E \l [(B_t-B_u)^3\|\mc {F}_u\r ]+3B_u\E \l [B_t^2\|\mc {F}_u\r ]-3B_u^2\E [B_t\|\mc {F}_u]-3B_u(t-u)\\ &=\E \l [(B_t-B_u)^3\r ]+3B_u\l (\E \l [B_t^2-t\|\mc {F}_u\r ]+t\r )-3B_u^3-3B_u(t-u)\\ &=0+3B_u\l (B_u^2-u+t\r )-3B_u^3-3B_u(t-u)\\ &=0. \end{align*} Here we use several applications of the fact that \(B_t-B_u\) is independent of \(\mc {F}_u\), whilst \(B_u\) is \(\mc {F}_u\) measurable. We use also that \(\E [Z^3]=0\) where \(Z\sim N(0,\sigma ^2)\), which comes from part (c) of 11.4 (or use that the normal distribution is symmetric about \(0\)), as well as that both \(B_t\) and \(B_t^2-t\) are martingales (from Lemmas 11.4.3 and 11.4.4).

• 11.7

  • (a) We have

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \sum _{k=0}^{n-1}(t_{k+1}-t_k) &=(t_n-t_{n-1})+(t_{n-1}-t_{n-2})+\ldots +(t_2-t_1)+(t_1-t_0)\\ &=t_n-t_0\\ &=t-0\\ &=t. \end{align*} This is known as a ‘telescoping sum’. The same method shows that \(\sum _{k=0}^{n-1}(B_{t_{k+1}}-B_{t_k})=B_t-B_0=0\).

  • (b) We need a bit more care for this one. We have

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} 0\leq \sum _{k=0}^{n-1}(t_{k+1}-t_k)^2 &\leq \sum _{k=0}^{n-1}(t_{k+1}-t_k)\l (\max _{j=0,\ldots ,n-1}|t_{j+1}-t_j|\r )\\ &= \l (\max _{j=0,\ldots ,n-1}|t_{j+1}-t_j|\r ) \sum _{k=0}^{n-1}(t_{k+1}-t_k)\\ &= \l (\max _{j=0,\ldots ,n-1}|t_{j+1}-t_j|\r )t. \end{align*} Here, the last line is deduced using part (a). Letting \(n\to 0\) we have \(\max _{j=0,\ldots ,n-1}|t_{j+1}-t_j|\to 0\), so the right hand side of the above tends to zero as \(n\to \infty \). Hence, using the sandwich rule, we have that \(\sum _{k=0}^{n-1}(t_{k+1}-t_k)^2\to 0\).

  • (c) Using the properties of Brownian motion, \(B_{t_k+1}-B_{t_k}\sim N(0,t_{k+1}-t_k)\) so from exercise 11.4 we have

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \E \l [\sum \limits _{k=0}^{n-1}(B_{t_k+1}-B_{t_k})^2\r ] &=\sum \limits _{k=0}^{n-1}\E \l [(B_{t_k+1}-B_{t_k})^2\r ]\\ &=\sum \limits _{k=0}^{n-1}(t_{k+1}-t_k)\\ &=t. \end{align*} Here, the last line follows by part (a).

    For the last part, the properties of Brownian motion give us that each increment \(B_{t_{k+1}}-B_{t_k}\) is independent of \(\mc {F}_{t_k}\). In particular, the increments \(B_{t_{k+1}}-B_{t_k}\) are independent of each other. So, using exercise 11.4,

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \var \l (\sum \limits _{k=0}^{n-1}(B_{t_k+1}-B_{t_k})^2\r ) &=\sum \limits _{k=0}^{n-1}\var \l ((B_{t_k+1}-B_{t_k})^2\r )\\ &=\sum \limits _{k=0}^{n-1}2(t_{k+1}-t_k)^2 \end{align*} which tends to zero as \(n\to \infty \), by the same calculation as in part (b).

• 11.8

  • (a) Let \(y\geq 1\). Then

    \(\seteqnumber{0}{C.}{0}\)

    \begin{align*} \P \l [B_t\geq y\r ] &=\int _y^\infty \frac {1}{\sqrt {2\pi t}}e^{-\frac {z^2}{2t}}\,dz\\ &\leq \int _y^\infty \frac {1}{\sqrt {2\pi t}}y e^{-\frac {z^2}{2t}}\,dz\\ &\leq \int _y^\infty \frac {1}{\sqrt {2\pi t}}z e^{-\frac {z^2}{2t}}\,dz\\ &=\frac {1}{\sqrt {2\pi t}}\l [-t e^{-\frac {z^2}{2t}}\r ]_{z=y}^\infty \\ &=\sqrt {\frac {t}{2\pi }}e^{-\frac {y^2}{2t}}. \end{align*} Putting \(y=t^\alpha \) where \(\alpha >\frac 12\) we have

    \(\seteqnumber{0}{C.}{0}\)

    \begin{equation} \label {eq:bm_asymp_1} \P [B_t\geq t^\alpha ]\leq \sqrt {\frac {t}{2\pi }}e^{-\frac 12t^{2\alpha -1}}. \end{equation}

    Since \(2\alpha -1\geq 0\), the exponential term dominates the square root, and right hand side tends to zero as \(t\to \infty \).

    If \(\alpha =\frac 12\) then we can use an easier method. Since \(B_t\sim N(0,t)\), we have \(t^{-1/2}B_t\sim N(0,1)\) and hence

    \[\P [B_t\geq t^{1/2}]=\P [N(0,1)\geq 1]\in (0,1),\]

    which is independent of \(t\) and hence does not tend to zero as \(t\to \infty \). Note that we can’t deduce this fact using the same method as for \(\alpha >\frac 12\), because (C.1) only gives us an upper bound on \(\P [B_t\geq t^{\alpha }]\).

  • (b) For this we need a different technique. For \(y\geq 0\) we integrate by parts to note that

    \(\seteqnumber{0}{C.}{1}\)

    \begin{align*} \int _y^\infty \frac {1}{\sqrt {2\pi t}}e^{-\frac {-z^2}{2t}}\,dz &=\frac {1}{\sqrt {2\pi t}}\int _y^\infty \frac {1}{z} z e^{-\frac {-y^2}{2t}}\,dz\\ &=\frac {1}{\sqrt {2\pi t}}\l (\l [-\frac {t}{z}e^{-\frac {z^2}{2t}}\r ]_{z=y}^\infty -\int _y^\infty \frac {t}{z^2}e^{-\frac {z^2}{2t}}\r )\,dz\\ &\leq \frac {1}{\sqrt {2\pi t}}\l (\l [-\frac {t}{z}e^{-\frac {z^2}{2t}}\r ]_{z=y}^\infty \r )\\ &= \frac {1}{\sqrt {2\pi t}} \frac {t}{y}e^{-\frac {y^2}{2t}}\\ &= \frac {t}{\sqrt {2\pi }} \frac {1}{y}e^{-\frac {y^2}{2t}} \end{align*} Using the symmetry of normal random variables about \(0\), along with this inequality, we have

    \(\seteqnumber{0}{C.}{1}\)

    \begin{align*} \P [|B_t|\geq a] &=\P [B_t\geq a]+\P [B_t\leq -a]\\ &=2\P [B_t\geq a]\\ &\leq 2 \frac {t}{\sqrt {2\pi }} \frac {1}{a}e^{-\frac {a^2}{2t}}. \end{align*} As \(t\searrow 0\), the exponential term tends to \(0\), which dominates the \(\sqrt {t}\), meaning that \(\P [|B_t|\geq a]\to 0\) as \(t\searrow 0\). That is, \(B_t\to 0\) in probability as \(t\searrow 0\).

Chapter 12

• 12.1 From (12.8) we have both \(\int _0^t 1\,dB_u=B_t\) and \(\int _0^s\,dB_u=B_s\), and using (12.6) we obtain

  \[\int _u^t1\,dB_u=\int _0^t1\,dB_u-\int _0^v1\,dB_u=B_t-B_v.\]

• 12.2 Since \(B_t\) is adapted to \(\mc {F}_t\), we have that \(e^{B_t}\) is adapted to \(\mc {F}_t\). Since \(B_t\) is a continuous stochastic process and \(\exp (\cdot )\) is a continuous function, \(e^{B_t}\) is also continuous. From (11.2) we have that

  \(\seteqnumber{0}{C.}{1}\)

  \begin{align*} \int _0^t\E \l [\l (e^{B_u}\r )^2\r ]\,du &=\int _0^t\E \l [e^{2B_u}\r ]\,du\\ &=\int _0^t e^{\frac 12(2^2)u}\,du\\ &= \int _0^te^{2u}\,du<\infty . \end{align*} Therefore, \(e^{B_t}\in \mc {H}^2\).

• 12.3

  • (a) We have

    \[\E \l [e^{\frac {Z^2}{2}}\r ]=\frac {1}{\sqrt {2\pi }}\int _{-\infty }^\infty e^{\frac {z^2}{2}}e^{\frac {-z^2}{2}}\,dz=\frac {1}{\sqrt {2\pi }}\int _{-\infty }^\infty 1\,dz =\infty .\]

  • (b) Using the scaling properties of normal distributions, \(t^{-1/2}B_t\) has a \(N(0,1)\) distribution for all \(t\). Hence, if we set \(F_t=t^{-1/2}B_t\) then by part (a) we have

    \[\int _0^t\E \l [e^{\frac {1}{2}F_t^2}\r ]\,du=\int _0^t\infty \,du\]

    which is not finite. Note also that \(F_t\) is adapted to \(\mc {F}_t\). Since \(e^t\), \(t^2\), \(t^{-1/2}\) and \(B_t\) are all continuous, so is \(e^{\frac {1}{2}F_t^2}\). Hence \(e^{\frac {1}{2}F_t^2}\) is an example of a continuous, adapted stochastic process that is not in \(\mc {H}^2\).

    Note that we can’t simply use the stochastic process \(F_t=Z\), because we have nothing to tell us that \(Z\) is \(\mc {F}_t\) measurable.

• 12.4 We have

  \(\seteqnumber{0}{C.}{1}\)

  \begin{align*} \E [X_t] &=\E [2]+\E \l [\int _0^t t+B_u^2\,du\r ]+\E \l [\int _0^t B_u^2\,d B_u\r ]\\ &=2+\int _0^tt+\E [B_u^2]\,du+0\\ &=2+t^2+\int _0^t u\,du\\ &=2+t^2+\frac {t^2}{2}\\ &=2+\frac {3t^2}{2}. \end{align*}

• 12.5

  • (a) \(X_t=0+\int _0^t0\,du+\int _0^t0\,dB_u\) so \(X_t\) is an Ito process.

  • (b) \(Y_t=0+\int _0^t2u\,du+\int _0^t1\,dB_u\) by (12.8), so \(Y_t\) is an Ito process.

  • (c) A symmetric random walk is a process in discrete time, and is therefore not an Ito process.

• 12.6 We have

  \(\seteqnumber{0}{C.}{1}\)

  \begin{align*} \E [V_t] &=\E [e^{-kt}v]+\sigma e^{-kt}\E \l [\int _0^t e^{ks}\,dB_s\r ]\\ &=e^{-kt}v. \end{align*} Here we use Theorem 12.2.1 to show that the expectation of the \(dB_u\) integral is zero. In order to calculate \(\var (V_t)\) we first calculate

  \(\seteqnumber{0}{C.}{1}\)

  \begin{align*} \E \l [V_t^2\r ] &=\E [e^{-2kt}v^2]+2\sigma e^{-kt}\E \l [\int _0^t e^{ks}\,dB_s\r ]+\sigma ^2 e^{-2kt}\E \l [\l (\int _0^t e^{ks}\,dB_s\r )^2\r ]\\ &=e^{-2kt}v^2+0+\sigma ^2 e^{-2kt}\int _0^t \E \l [(e^{ks})^2\r ]\,du\\ &=e^{-2kt}v^2+\sigma ^2 e^{-2kt}\int _0^t e^{2ku}\,du\\ &=e^{-2kt}v^2+\sigma ^2 e^{-2kt}\frac {1}{2k}\l (e^{2kt}-1\r )\\ &=e^{-2kt}v^2+\frac {\sigma ^2}{2k}\l (1-e^{-2kt}\r ) \end{align*} Again, we use Theorem 12.2.1 to calculate the final term on the first line. We obtain that

  \(\seteqnumber{0}{C.}{1}\)

  \begin{align*} \var (V_t)&= \E [V_t^2]-\E [V_t]^2\\ &=\frac {\sigma ^2}{2k}\l (1-e^{-2kt}\r ). \end{align*}

• 12.7 We have

  \[X_t=\mu t+\int _0^t \sigma _u\,dB_u.\]

  Since \(M_t=\int _0^t \sigma _u\,dB_u\) is a martingale (by Theorem 12.2.1), we have that \(M_t\) is adapted and in \(L^1\), and hence also \(X_t\) is adapted and in \(L^1\). For \(v\leq t\) we have

  \(\seteqnumber{0}{C.}{1}\)

  \begin{align*} \E \l [X_t\|\mc {F}_v\r ]&=\mu t+\E \l [M_t\|\mc {F}_v\r ]\\ &=\mu t+M_v\\ &=\mu t+\int _0^v\sigma _u\,dB_u\\ &\geq \mu v+\int _0^v\sigma _u\,dB_u\\ &=X_v. \end{align*} Hence, \(X_t\) is a submartingale.

• 12.8

  • (a) Taking \(F_t=0\), we have \(\E [F_t]=\) and \(\int _0^tF_s\,ds=0\), hence \(\int _0^t \E [F_s]\,ds=\E [\int _0^t F_s\,dB_s]=0\).

  • (b) Taking \(F_t=1\), we have \(\E [F_t]=1\) and \(\int _0^tF_s\,ds=t\), hence \(\int _0^t \E [F_s]\,ds=t\) and \(\E [\int _0^t F_s\,dB_s]=\E [B_t]=0\).

• 12.9

  • (a) We have \((|X|-|Y|)^2\geq 0\), so \(2|XY|\leq X^2+Y^2\), which by monotonicity of \(\E \) means that \(2\E [|XY|]\leq \E [X^2]+\E [Y^2]\). Using the relationship between \(\E \) and \(|\cdot |\) we have

    \[2|\E [XY]|\leq 2\E [|XY|]\leq \E [X^2]+\E [Y^2].\]

  • (b) Let \(X_t,Y_t\in \mc {H}^2\) and let \(\alpha ,\beta \in \R \) be deterministic constants. We need to show that \(Z_t\alpha X_t+\beta Y_t\in \mc {H}^2\). Since both \(X_t\) and \(Y_t\) are continuous and adapted, \(Z_t\) is also both continuous and adapted. It remains to show that (12.5) holds for \(Z_t\). With this in mind we note that

    \[Z_t^2=\alpha ^2X_t^2+2\alpha \beta X_tY_t+\beta ^2Y_t^2\]

    and hence that

    \(\seteqnumber{0}{C.}{1}\)

    \begin{align*} |\E [Z_t^2]|&=\l |\alpha ^2\E [X_t^2]+2\alpha \beta \E [X_tY_t]+\beta ^2\E [Y_t^2]\r |\\ &\leq \alpha ^2\E [X_t^2]+2|\alpha \beta |\,\l |\E [X_tY_t]\r |+\beta ^2\E [Y_t^2]\\ &\leq \alpha ^2\E [X_t^2]+|\alpha \beta |(\E [X_t^2]+\E [Y_t^2])+\beta ^2\E [Y_t^2]\\ &=(\alpha ^2+|\alpha \beta |)\E [X_t^2]+(\beta ^2+|\alpha \beta |)|\E [Y_t^2]. \end{align*} where we use part (a) to deduce the third line from the second. Hence,

    \(\seteqnumber{0}{C.}{1}\)

    \begin{align*} \int _0^t\E [Z_u^2]\,du &\leq \int _0^t (\alpha ^2+|\alpha \beta |)\E [X_u^2]+(\beta ^2+|\alpha \beta |)|\E [Y_u^2]\,du\\ &=(\alpha ^2+|\alpha \beta |)\int _0^t \E [X_u^2]\,du+(\beta ^2+|\alpha \beta |)\int _0^t \E [Y_u^2]\,du<\infty \end{align*} as required. The final line is \(<\infty \) because \(X_t,Y_t\in \mc {H}^2\).

• 12.10 We have \(I_F(t)=\sum \limits _{i=1}^n F_{t_{i-1}}[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}].\) We are looking to show that

  \(\seteqnumber{0}{C.}{1}\)

  \begin{equation} \label {eq:ii1} \E [I_F(t)^2]=\int _0^t \E [F_u^2]\,du. \end{equation}

  On the right hand side we have

  \(\seteqnumber{0}{C.}{2}\)

  \begin{align} \int _0^t \E [F_u^2]\,du &=\sum \limits _{i=1}^{m}\int _{t_{i-1\wedge t}}^{t_i\wedge t}\E [F_u^2]\,du\notag \\ &=\sum \limits _{i=1}^m (t_i\wedge t-t_{i-1}\wedge t)\E [F_{t_{i-1}}^2]\label {eq:ii2} \end{align} because \(F_t\) is constant during each time interval \([t_{i-1}\wedge t,t_i\wedge t)\). On the left hand side of (C.2) we have

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \E [I_F(t)^2] &=\E \l [\l (\sum \limits _{i=1}^m F_{t_{i-1}}[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]\r )^2\r ]\\ &=\E \l [\sum \limits _{i=1}^m F_{t_{i-1}}^2[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]^2+2\sum \limits _{i=1}^m\sum \limits _{j=1}^{i-1}F_{t_{i-1}}F_{t_{j-1}}[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}][B_{t_j\wedge t}-B_{t_{j-1}\wedge t}]\r ]\\ &=\sum \limits _{i=1}^m \E \l [F_{t_{i-1}}^2[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]^2\r ]+2\sum \limits _{i=1}^m\sum \limits _{j=1}^{i-1}\E \l [F_{t_{i-1}}F_{t_{j-1}}[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}][B_{t_j\wedge t}-B_{t_{j-1}\wedge t}]\r ] \end{align*} In the first sum, using the tower rule, taking out what is known, independence, and then the fact that \(\E [B_t^2]=t\), we have

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \E \l [F_{t_{i-1}}^2[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]^2\r ] &=\E \l [\E \l [F_{t_{i-1}}^2[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]^2\|\mc {F}_{t_{i-1}}\r ]\r ]\\ &=\E \l [F_{t_{i-1}}^2\E \l [[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]^2\|\mc {F}_{t_{i-1}}\r ]\r ]\\ &=\E \l [F_{t_{i-1}}^2\E \l [[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}]^2\r ]\r ]\\ &=\E \l [F_{t_{i-1}}^2(t_{i}\wedge t-t_{i-1}\wedge t)\r ] \end{align*} In the second sum, since \(j<i\) we have \(t_{j-1}\leq t_i\), so using the tower rule, taking out what is known, and then the martingale property of Brownian motion, we have

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \E \l [F_{t_{i-1}}F_{t_{j-1}}[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}][B_{t_j\wedge t}-B_{t_{j-1}\wedge t}]\r ] &=\E \l [\E \l [F_{t_{i-1}}F_{t_{j-1}}[B_{t_i\wedge t}-B_{t_{i-1}\wedge t}][B_{t_j\wedge t}-B_{t_{j-1}\wedge t}]\|\mc {F}_{t_{i-1}}\r ]\r ]\\ &=\E \l [F_{t_{j-1}}[B_{t_j\wedge t}-B_{t_{j-1}\wedge t}]F_{t_{i-1}}\l (\E \l [B_{t_i\wedge t}\|\mc {F}_{t_{i-1}}\r ]-B_{t_{i-1}\wedge t}\r )\r ]\\ &=\E \l [F_{t_{j-1}}[B_{t_j\wedge t}-B_{t_{j-1}\wedge t}]F_{t_{i-1}}\l (B_{t_{i-1}\wedge t}-B_{t_{i-1}\wedge t}\r )\r ]\\ &=0. \end{align*} Therefore,

  \[\E [I_F(t)^2]=\sum \limits _{i=1}^m\E \l [F_{t_{i-1}}^2(t_{i}\wedge t-t_{i-1}\wedge t)\r ]\]

  which matches (C.3) and completes the proof.

Chapter 13

• 13.1

  • (a) \(X_t=X_0+\int _0^t2u\,du+\int _0^tB_u\,dB_u\).

  • (b) \(Y_T=Y_t+\int _t^T u\,du\).

  By using the fundamental theorem of calculus, we obtain that \(Y\) satisfies the differential equation \(\frac {d Y_t}{dt}=t\). Using equation (13.6) from Example 13.1.2, we have that

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} X_t=X_0+t^2+\frac {B_t^2}{2}-\frac {t}{2} \end{align*} which is not differentiable because \(B_t\) is not differentiable.

• 13.2 We have \(Z_t=f(t,X_t)\) where \(f(t,x)=t^3x\) and \(dX_t=\alpha \,dt+\beta \,dB_t\). By Ito’s formula,

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} dZ_t &=\l \{(0)+(t^2)\l (\frac {-1}{X_t^2}\r )+\frac 12(B_t)^2\l (\frac {2}{X_t^3}\r )\r \}\,dt+(B_t)\l (\frac {-1}{X_t^2}\r )\,B_t\\ &=\l (B_t^2Z_t^{3}-t^2Z_t^2\r )\,dt-B_tZ_t^2\,dB_t. \end{align*}

• (d) We have

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \E [B_t^n] &=\int _0^t\frac {n(n-1)\E [B_u^{n-2}]}{2}\,du+0\\ &=\frac {n(n-1)}{2}\int _0^t\E [B_u^{n-2}]\,du \end{align*} as required.

  Let us check that this formula agrees with the results of exercise 11.4 part (c). When \(n\) is odd, we had obtained \(\E [B^n_t]=0\), so this case is trivial. When \(n\) is even, we had obtained \(\E [B^n_t]=t^{n/2}(n-1)(n-3)\ldots (1)\). Note that

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \frac {n(n-1)}{2}\int _0^t u^{(n-2)/2}(n-3)(n-5)\ldots (1)\,du &= \frac {n(n-1)}{2} \frac {t^{n/2}}{n/2}(n-3)(n-5)\ldots (1)\,du \\ &= t^{n/2}(n-1)(n-3)\ldots (1) \end{align*} as required.

• 13.5

  • (a) By Ito’s formula, with \(f(t,x)=e^{t/2}\cos x\), we have

    \(\seteqnumber{0}{C.}{3}\)

    \begin{align*} dX_t &=\l (\frac 12e^{t/2}\cos (B_t)+(0)\l (-e^{t/2}\sin (B_t)\r )+\frac 12(1^2)(-e^{t/2}\cos (B_t))\r )\,dt+(1)\l (-e^{t/2}\sin (B_t)\r )\,dB_t\\ &=-e^{t/2}\sin (B_t)\,dB_t. \end{align*} Hence \(X_t=X_0-\int _0^te^{u/2}\sin (B_u)\,dB_u\), which is martingale by Theorem 12.2.1.

  • (b) By Ito’s formula, with \(f(t,x)=(x+t)e^{-x-t/2}\) we have

    \(\seteqnumber{0}{C.}{3}\)

    \begin{align*} \E [Y_t]&=Y_0+\E \l [\int _0^t 4(1+s)X_t+(B_s)^2\,ds\r ]+0\\ &=1+\int _0^t4(1+s)\E [X_s]+\E [B_s^2]\,ds\\ &=1+\int _0^t4(1+s)^3+s\,ds\\ &=1+\l [(1+s)^4+\tfrac {s^2}{2}\r ]_{s=0}^t\\ &=(1+t)^4+\tfrac {t^2}{2} \end{align*} Hence, using that \(\E [X_t^2]=\E [Y_t]\),

    \(\seteqnumber{0}{C.}{3}\)

    \begin{align*} \var (X)&=\E [X_t^2]-\E [X_t]^2\\ &=(1+t)^4+\tfrac {t^2}{2}-(1+t)^4\\ &=\tfrac {t^2}{2}. \end{align*}

  • (c) If we change the \(dB_t\) coefficient then we won’t change the mean, because we can see from (a) that \(\E [X_t]\) depends only on the \(dB_t\) coefficient. However, as we can see from part (b), the variance depends on both the \(dt\) and \(dB_t\) terms, so will typically change if we alter the \(dB_t\) coefficient.

• 13.8 In integral form, we have

  \[X_t=X_0+\int _0^t\alpha X_u\,du+\int _0^t \sigma _u\,dB_u.\]

  Taking expectations, swapping \(\int \,du\) with \(\E \), and recalling from Theorem 12.2.1 that Ito integrals are zero mean martingales, we obtain

  \[\E [X_t]=\E [X_0]+\int _0^t \alpha \E [X_u]\,du.\]

  Applying the fundamental theorem of calculus, if we set \(x_t=\E [X_t]\), we obtain

  \[\frac {d x_t}{dt}=\alpha x_t\]

  which has solution \(x_t=Ce^{\alpha t}\). Putting in \(t=0\) shows that \(C=\E [X_0]=1\), hence

  \[\E [X_t]=e^{\alpha t}.\]

• 13.9 We have \(X_t=X_0+\int _0^t X_s\,dB_s\). Since Ito integrals are zero mean martingales, this means that \(\E [X_t]=\E [X_0]=1\). Writing \(Y_t=X_t^2\) and using Ito’s formula,

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} dY_t &=\l (0+(0)(2X_t)+\tfrac 12(X_t)^2(2)\r )\,dt+(X_t)(2X_t)\,dB_t\\ &=(X_t^2)\,dt+2X_t^2\,dB_t.\\ &=Y_t\,dt+2Y_t\,dB_t \end{align*} Writing in integral form and taking expectations, we obtain

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \E [Y_t] &=1+\int _0^t \E [Y_s]\,ds+0. \end{align*} Hence, by the fundamental theorem of calculus, \(f(t)=\E [Y_t]\) satisfies the differential equation \(f'(t)=f(t)\). The solution of this differential equation is \(f(t)=Ae^t\). Since \(\E [Y_0]=1\) we have \(A=1\) and thus \(\E [Y_t]=e^t\). Hence,

  \[\var (X_t)=\E [X_t^2]-\E [X_t]^2=\E [Y_t]-1=e^t-1.\]

• 13.10

  Recall that \(\cov (X_s, X_t)=\E [(X_t-\E [X_t])(X_s-\E [X_s])\). From (13.12) we have

  \[\E [X_t]=\E [e^{-\theta t}(X_t-\mu )]+\E \l [\int _0^t e^{-\theta (t-u)}\,dB_u\r ]=\E [e^{-\theta t}(X_t-\mu )]+0,\]

  because Ito integrals are zero mean martingales. Thus \(X_t-\E [X_t]=\int _0^t \sigma e^{\theta (u-t)}\,d B_u\). We can now calculate

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} \cov (X_s, X_t) &= \text {Cov}\biggl ( \int _0^s \sigma \, e^{\theta (u-s)} dB_u \, , \, \int _0^t \sigma \, e^{\theta (v-t)} dB_v \biggr ) \\ &= \mathbb {E}\biggl [ \l (\int _0^s \sigma \, e^{\theta (u-s)} dB_u \r )\l (\int _0^t \sigma \, e^{\theta (v-t)} dB_v\r ) \biggr ] \\ &= \sigma ^2 e^{-\theta (s+t)}\, \mathbb {E}\biggl [ \l (\int _0^s e^{\theta u} dB_u \r )\l ( \int _0^t e^{\theta v} dB_v \r )\biggr ] \\ &= \sigma ^2 e^{-\theta (s+t)}\, \mathbb {E}\biggl [ \biggl ( \int _0^{s} e^{\theta u} dB_u + \int _{s}^{t} e^{\theta u} dB_u \biggr ) \l (\int _0^{s} e^{\theta v} dB_v \r )\biggr ]\\ &= \sigma ^2 e^{-\theta (s+t)}\, \mathbb {E}\biggl [ \biggl ( \int _0^{s} e^{\theta u} dB_u \biggr )^2 \biggr ] + \E \l [\l (\int _0^{s} e^{\theta v} dB_v\r )\l (\int _s^t e^{\theta u} dB_u \r )\r ]\\ &= \sigma ^2 e^{-\theta (s+t)}\, \int _0^{s} e^{2 \theta u} du + \E \l [\int _0^{s} e^{\theta v} dB_v\r ]\E \l [\int _s^t e^{\theta u} dB_u \r ]\\ &= \frac {\sigma ^2}{2\theta } e^{-\theta (s+t)}\l ( e^{2\theta s} - 1 \r ) + 0. \end{align*} In the above, the second line and final lines follow because Ito integrals have zero mean. The penultimate line follows because \(\int _0^{s} e^{\theta v} dB_v\) and \(\int _s^t e^{\theta u} dB_u\) are independent. This fact follows from the independence property in Theorem 11.2.1 (which defines Brownian motion), which implies that \(\sigma (B_v-B_u\-v\geq u\geq s)\) and \(\sigma (B_v-B_u\-s\geq v\geq u)\) are independent. Note that from (12.3) we know that \(\int _a^b F_u\,dB_s\) only depends on increments of Brownian motion between times \(a\) and \(b\). (The same fact can be deduced from the Markov property from Section 14.2.)

  Hence \(\var (X_t)=\frac {\sigma ^2}{2\theta }e^{-\theta (2t)}(e^{2\theta t}-1)=\frac {\sigma ^2}{2\theta }(1-e^{-2\theta t})\). It follows immediately that \(\var (X_t)\to \frac {\sigma ^2}{2\theta }\) as \(t\to \infty \).

• 13.11

  • (a) Applying Ito’s formula to \(Z_t=B_t^3\), with \(f(t,x)=x^3\), we have

    \(\seteqnumber{0}{C.}{3}\)

    \begin{align*} dZ_t&=\l (0+(0)(3B_t^2)+\frac 12(1^2)(6B_t)\r )\,dt+(1)(3B_t^2)\,dB_t\\ &=3B_t\,dt+3B_t^2\,dt \end{align*} and substituting in for \(Z\) we obtain

    \[dZ_t=3Z_t^{1/3}\,dt+3Z_t^{2/3}\,dB_t\]

    as required.

  • (b) Another solution is the (constant, deterministic) solution \(X_t=0\).

• 13.12 Equation (13.9) says that

  \[X_t=X_0\exp \l ((\alpha -\tfrac 12\sigma ^2)t+\sigma B_t\r ).\]

  Using Ito’s formula, with \(f(t,x)=X_0\exp \l ((\alpha -\tfrac 12\sigma ^2)t+\sigma x\r )\) we obtain

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} dX_t&=\l ((\alpha -\tfrac 12\sigma ^2)X_t+(0)(\sigma X_t)+\frac 12(1^2)(\sigma ^2 X_t)\r )\,dt+\,(1)(\sigma X_t)dB_t\\ &=\alpha X_t \,dt+\sigma X_t\,dB_t \end{align*} and thus \(X_t\) solves (13.8).

• 13.13 Equation (13.14) says that

  \[X_t=X_0\exp \l (\int _0^t\sigma _u\,dB_u -\frac {1}{2}\int _0^t\sigma _u^2\,du\r )\]

  We need to arrange this into a form where we can apply Ito’s formula. We write

  \[X_t=X_0\exp \l (Y_t -\frac {1}{2}\int _0^t\sigma _u^2\,du\r )\]

  where \(dY_t=\sigma _t\,dB_t\) with \(Y_0=0\). We now have \(X_t=f(t,Y_t)\) where \(f(t,y)=X_0\exp \l (y-\frac 12\int _0^t\sigma _u\,du\r )\), so from Ito’s formula (and the fundamental theorem of calculus) we obtain

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} dX_t&=\l (-\frac 12\sigma _t^2X_t+(0)(X_t)+\frac 12(\sigma _t^2)(X_t)\r )\,dt+(\sigma _t)(X_t)\,dB_t\\ &=\sigma _t X_t\,dB_t. \end{align*} Hence, \(X_t\) solves (13.13).

• 13.14

  • (a) This is essentially Example 3.3.9 but in continuous time. By definition of conditional expectation (i.e. Theorem 3.1.1) we have that \(M_t\in L^1\) and that \(M_t\in \mc {F}_t\). It remains only to use the tower property to note that for \(0\leq u\leq t\) we have

    \[\E [M_t|\mc {F}_u]=\E [\E [Y\|\mc {F}_t]\mc {F}_u]=\E [Y\|\mc {F}_u]=M_u.\]

  • (b)

    • (i) Note that \(M_0=\E [B_T^2\|\mc {F}_0]=\E [B_T^2]=T\). We showed in Lemma 11.4.4 that \(B_t^2-t\) was a martingale, hence

      \(\seteqnumber{0}{C.}{3}\)

      \begin{align*} \E [B_T^2\|\mc {F}_t] &=\E [B_T^2-T+T\|\mc {F}_t]\\ &=B_t^2-t+T\\ \end{align*} Using (13.6), this gives us that

      \[\E [B_T^2\|\mc {F}_t]=2\int _0^tB_u\,dB_u+t-t+T\]

      so we obtain

      \[M_t=T+\int _0^t 2B_u\,dB_u\]

      and we can take \(h_t=2B_t\).

    • (ii) Note that \(M_0=\E [B_T^3\|\mc {F}_0]=\E [B_T^3]=0\). We showed in 11.6 that \(B_t^3-3tB-t\) was a martingale. Hence,

      \(\seteqnumber{0}{C.}{3}\)

      \begin{align*} \E [B_T^3\|\mc {F}_t]&=\E [B_T^3-3TB_T+3TB_T\|\mc {F}_t]\\ &=B_t^3-3tB_t+3TB_t. \end{align*} Using Ito’s formula on \(Z_t=B_t^3\), we obtain \(dZ_t=\l \{0+(0)(3B_t^2)+\frac 12(1^2)(6B_t)\r \}\,dt+(1)(3B_t^2)\,dB_t\) so as

      \[B_t^3=0+\int _0^t3B_u\,du+\int _0^t3B_u^2\,dB_u.\]

      Also, from 13.6 we have

      \[tB_t=\int _0^tB_u\,du+\int _0^t u\,dB_u,\]

      so as

      \(\seteqnumber{0}{C.}{3}\)

      \begin{align*} \E [B_T^3\|\mc {F}_t] &=3\int _0^tB_u\,du+3\int _0^tB_u^2\,dB_u-3\l (\int _0^tB_u\,du+\int _0^t u\,dB_u\r )+3TB_t\\ &=3\int _0^tB_u^2\,dB_u-3\int _0^t u\,dB_u+3T\int _0^t1\,dB_u\\ &=\int _0^t3B_u^2-3u+3T\,dB_u. \end{align*} We can take \(h_t=3B_t^2-3t+3T\).

    • (iii) Note that \(M_0=\E [e^{\sigma B_T}\|\mc {F}_0]=\E [e^{\sigma B_T}]=e^{\frac 12\sigma ^2T}\) by (11.2) and the scaling properties of normal random variables. We showed in 11.6 that \(e^{\sigma B_t-\frac 12\sigma ^2t}\) was a martingale. Hence,

      \(\seteqnumber{0}{C.}{3}\)

      \begin{align*} \E [e^{\sigma B_T}\|\mc {F}_t] &=\E [e^{\sigma B_T-\frac 12\sigma ^2T}e^{\frac 12\sigma ^2T}\|\mc {F}_t]\\ &=e^{\sigma B_t-\frac 12\sigma ^2t}e^{\frac 12\sigma ^2T}\\ &=e^{\sigma B_t-\frac 12\sigma ^2(T-t)}. \end{align*} Applying Ito’s formula to \(Z_t=e^{\sigma B_t-\frac 12\sigma ^2(T-t)}\) gives that

      \(\seteqnumber{0}{C.}{3}\)

      \begin{align*} dZ_t&=\l (-\frac 12\sigma ^2Z_t+(0)(\sigma Z_t)+\frac 12(1^2)(\sigma ^2 Z_t)\r )\,dt+(1)(\sigma Z_t)\,dB_t\\ &=\sigma Z_t dB_t \end{align*} so we obtain that

      \[Z_t=Z_0+\int _0^t\sigma Z_u\,dB_u.\]

      Substituting in for \(Z_t\) we obtain

      \[\E [e^{\sigma B_T}\|\mc {F}_t]=e^{\frac 12\sigma ^2T}+\int _0^t\sigma Z_u\,dB_u\]

      so we can take \(h_t=\sigma Z_t=\sigma e^{\sigma B_t-\frac 12\sigma ^2(T-t)}\).

Chapter 14

• 14.1 We have \(\alpha (t,x)=-2t\), \(\beta =0\) and \(\Phi (x)=e^x\). By Lemma 14.1.2 the solution is given by

  \[F(t,x)=\E _{t,x}[e^{X_T}]\]

  where \(dX_u=-2u\,du+0\,dB_u=\,du\). This gives

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} X_T&=X_t-\int _t^T2u\,du\\ &=X_t-T^2+t^2. \end{align*} Hence,

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} F(t,x)&=\E _{t,x}\l [e^{X_t-t^2}\r ]\\ &=\E \l [e^{x-T^2+t^2}\r ]\\ &=e^{x}e^{-T^2+t^2}. \end{align*} Here we use that \(X_t=x\) under \(\E _{t,x}\).

• 14.2 We have \(\alpha =\beta =1\) and \(\Phi (x)=x^2\). By Lemma 14.1.2 the solution is given by

  \[F(t,x)=\E _{t,x}\l [X_T^2\r ]\]

  where \(dX_u=du+dB_u\). This gives

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} X_T&=X_t+\int _t^T\,du+\int _t^T\,dB_u\\ &=X_t+(T-t)+(B_T-B_t). \end{align*} Hence,

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align*} F(t,x)&=E_{t,x}[\l (X_t+(T-t)+(B_T-B_t)\r )^2]\\ &=\E \l [x^2+(T-t)^2+(B_T-B_t)^2+2x(T-t)+2x(B_T-B_t)+2(T-t)(B_T-B_t)\r ]\\ &=x^2+(T-t)^2+(T-t)+2x(T-t). \end{align*} Here we use that \(X_t=x\) under \(\E _{t,x}\) and that \(B_T-B_t\sim B_{T-t}\sim N(0,T-t).\)

• 14.3

  • (a) We have \(Z_t=F(t,X_t)+\gamma (t)\), where \(dX_t=\alpha (t,x)\,dt+\beta (t,x)\,dB_t\), so

    \(\seteqnumber{0}{C.}{3}\)

    \begin{align*} dZ_t&=\l (\frac {\p F}{\p t}+\frac {\p \gamma }{\p t}(t)+\alpha (t,x)\frac {\p F}{\p x}+\frac 12\beta (t,x)^2\frac {\p ^2 F}{\p x^2}\r )\,dt+\beta (t,x)\frac {\p F}{\p x}\,dB_t\\ &=\beta (t,x)\frac {\p F}{\p x}\,dB_t \end{align*} where as usual we have suppressed the \((t,X_t)\) arguments of \(F\) and its partial derivatives. Note that the term in front of the \(dt\) is zero because \(F\) satisfies (14.8).

  • (b) We use the same strategy as in the proof of Lemma 14.1.2. Writing out \(dZ_t\) in integral form over time interval \([t,T]\) we obtain

    \[Z_T=Z_t+\int _t^T\beta (u,x)\frac {\p F}{\p x}\,dB_u.\]

    Taking expectations \(\E _{t,x}\) gives us

    \[\E _{t,x}\l [F(T,X_T)+\gamma (T)\r ]=\E _{t,x}[F(t,X_t)+\gamma (t)]\]

    and noting that \(X_t=x\) under \(\E _{t,x}\), we have

    \[\E _{x,t}\l [F(T,X_T)\r ]+\gamma (T)=F(t,x)+\gamma (t).\]

    Using (14.9) we have \(F(T,X_T)=\Phi (X_T)\) and we obtain

    \[\E _{x,T}[\Phi (X_T)]+\gamma (T)-\gamma (t)=F(t,x)\]

    as required.

• 14.4 Consider (for example) the stochastic process

  \[M_t= \begin {cases} B_t & \text { for } t\leq 1,\\ B_t-B_{t-2} & \text { for }t> 1. \end {cases} \]

  We now consider \(M_t\) at time \(3\). The intuition is that \(\E [M_{3}\|\mc {F}_2]\) can see the value of \(B_1\), but that \(\sigma (M_2)=\sigma (B_2)\) and \(\E [M_{3}\|\sigma (M_2)]\) cannot see the value of \(B_1\).

  Formally: we have

  \(\seteqnumber{0}{C.}{3}\)

  \begin{align} \E [M_{3}\|\mc {F}_2] &=\E [B_{3}-B_{1}\|\mc {F}_2]\notag \\ &=B_2-B_1\label {eq:non_markov_1} \end{align} Here, we use that \(B_t\) is a martingale. However,

  \(\seteqnumber{0}{C.}{4}\)

  \begin{align} \E _{2,M_2}[M_{3}] &=\E [B_{3}-B_{1}\|\sigma (M_2)]\notag \\ &=\E [B_{3}-B_{1}\|\sigma (B_2-B_{0})]\notag \\ &=\E [B_{3}-B_{1}\|\sigma (B_2)]\notag \\ &=\E [B_{3}-B_2\|\sigma (B_2)]+\E [B_2\|\sigma (B_2)]-\E [B_{1}\|\sigma (B_2)]\notag \\ &=\E [B_{3}-B_2]+B_2-\E [B_{1}\|\sigma (B_2)]\notag \\ &=0+B_2-\E [B_{1}\|\sigma (B_2)]\notag \\ &=B_2-\E [B_{1}\|\sigma (B_2)]\label {eq:non_markov_2} \end{align} If we can show that (C.4) and (C.5) are not equal, then we have that \(M_t\) is not Markov. Their difference is \(D=\eqref {eq:non_markov_1}-\eqref {eq:non_markov_2}=\E [B_1\|\sigma (B_2)]-B_1\).

  We can write \(B_2=(B_2-B_1)+(B_1-B_0)\). By the properties of Brownian motion, \(B_2-B_1\) and \(B_1-B_0\) are independent and identically distributed. Hence, by symmetry, \(\E [B_2-B_1\|\sigma (B_2)]=\E [B_1-B_0\|\sigma (B_2)]\) and since

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} B_2&=\E [B_2\|\sigma (B_2)] =\E [B_2-B_1\|\sigma (B_2)]+\E [B_1-B_0\|\sigma (B_2)] \end{align*} we have that \(\E [B_2-B_1\|\sigma (B_2)]=\frac {B_2}{2}\). Hence

  \[D=\frac {B_2}{2}-B_1\]

  which is non-zero.

Chapter 15

• 15.1 We have

  \[\frac {\p f}{\p t}=0,\quad \frac {\p f}{\p s}=c,\quad \frac {\p ^2 f}{\p x^2}=0\]

  which, put into (15.10), gives \((0)+rs(c)+\frac 12s^2\sigma ^2(0)-r(cs)=0\). Similarly,

  \[\frac {\p g}{\p t}=rce^{rt},\quad \frac {\p g}{\p s}=0,\quad \frac {\p ^2 g}{\p x^2}=0\]

  which, put into (15.10), gives \((rce^{rt})+rs(0)+\frac 12s^2\sigma ^2(0)-r(ce^{rt})=0\).

• 15.2 We have

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} e^{-r(T-t)}\E ^\Q \l [\Phi (S_T)\|\mc {F}_t\r ] &=e^{-r(T-t)}\E ^\Q \l [K\r ]\\ &=Ke^{-r(T-t)}\\ \end{align*} because \(K\) is deterministic. By Theorem 15.3.1 this is the price of the contingent claim \(\Phi (S_T)\) at time \(t\).

  We can hedge the contingent claim \(K\) simply by holding \(Ke^{-rT}\) cash at time \(0\), and then waiting until time \(T\). While we wait, the cash increases in value according to (15.2) i.e. at continuous rate \(r\). So, this answer is not surprising.

• 15.3

  • (a) By Theorem 15.3.1 the price of the contingent claim \(\Phi (S_T)=\log (S_T)\) at time \(t\) is

    \(\seteqnumber{0}{C.}{5}\)

    \begin{align*} e^{-r(T-t)}\E ^\Q \l [\Phi (S_T)\|\mc {F}_t\r ] &=e^{-r(T-t)}\E ^\Q \l [\log (S_T)\|\mc {F}_t\r ]. \end{align*} Recall that, under \(\Q \), \(S_t\) is a geometric Brownian motion, with \(S_0=0\), drift \(r\) and volatility \(\sigma \). So from (15.20) we have \(S_T=S_te^{(r-\frac 12\sigma ^2)t+\sigma B_t}\). Hence,

    \(\seteqnumber{0}{C.}{5}\)

    \begin{align*} e^{-r(T-t)}\E ^\Q \l [\log (S_T)\|\mc {F}_t\r ] &=e^{-r(T-t)}\E ^\Q \l [\log (S_t)+(r-\tfrac 12\sigma ^2)(T-t)+\sigma (B_T-B_t)\|\mc {F}_t\r ]\\ &=e^{-r(T-t)}\l (\log (S_t)+(r-\tfrac 12\sigma ^2)(T-t)+\sigma \l (\E ^\Q [B_T\|\mc {F}_t]-B_t\r )\r )\\ &=e^{-r(T-t)}\l (\log (S_t)+(r-\tfrac 12\sigma ^2)(T-t)\r ). \end{align*} Here, we use that \(S_t,B_t\) are \(\mc {F}_t\) measurable, and that \((B_t)\) is a martingale.

    Putting in \(t=0\) we obtain

    \[e^{-rT}\l (\log (S_0)+(r-\tfrac 12\sigma ^2)T\r ),\]

  • (b) The strategy could be summarised as ‘write down \(\Phi (S_T)\), replace \(T\) with \(t=0\) and hope’. The problem is that if we buy \(\log s\) units of stock at time \(0\), then from (15.20) (with \(t=0\)) its value at time \(T\) will be \((\log s)\exp ((r-\frac 12\sigma ^2)T+\sigma B_T)\), which is not equal to \(\log S_T=\log s+(r-\frac 12\sigma ^2)T+\sigma B_T\).

    (In more formal terminology, the problem is that our excitable mathematician has assumed, incorrectly, that the \(\log \) function and the ‘find the price’ function commute with each other.)

• 15.4

  • (a) We have (in the risk neutral-world \(\Q \)) that \(dS_t=rS_t\,dt+\sigma S_t\,dB_t\). Hence, by Ito’s formula,

    \(\seteqnumber{0}{C.}{5}\)

    \begin{align*} dY_t&=\l ((0)+rS_t(\beta S_t^{\beta -1})+\frac 12\sigma ^2S_t^2(\beta (\beta -1)S_t^{\beta -2})\r )\,dt+\sigma S_t (\beta S_t^{\beta -1})dB_t\\ &=\l (r\beta +\tfrac 12\sigma ^2\beta (\beta -1)\r )Y_t\,dt+(\sigma \beta )Y_t\,dB_t. \end{align*} So \(Y_t\) is a geometric Brownian motion with drift \(r\beta +\frac 12\sigma ^2\beta (\beta -1)\) and volatility \(\sigma \beta \).

  • (b) Applying (15.20) and replacing the drift and volatility with those from part (a), we have that

    \(\seteqnumber{0}{C.}{5}\)

    \begin{align*} Y_T &=Y_t\exp \l (\l (r\beta +\tfrac 12\sigma ^2\beta (\beta -1)-\tfrac 12\sigma ^2\beta ^2\r )(T-t)+\sigma \beta (B_T-B_t)\r )\\ &=Y_t\exp \l (\l (r\beta -\tfrac 12\sigma ^2\beta \r )(T-t)+\sigma \beta (B_T-B_t)\r ). \end{align*} By Theorem 15.3.1, the arbitrage free price of the contingent claim \(Y_t=\Phi (S_T)\) at time \(t\) is

    \(\seteqnumber{0}{C.}{5}\)

    \begin{align*} e^{-r(T-t)}\E ^\Q \l [Y_T\|\mc {F}_t\r ] &=e^{-r(T-t)}\E ^\Q \l [S_t^\beta \exp \l (\l (r\beta -\tfrac 12\sigma ^2\beta \r )(T-t)+\sigma \beta (B_T-B_t)\r )\|\mc {F}_t\r ]\\ &=e^{-r(T-t)}S_t^\beta e^{(r\beta -\frac 12\sigma ^2\beta )(T-t)}\E ^\Q \l [e^{\sigma \beta (B_T-B_t)}\|\mc {F}_t\r ]\\ &=e^{-r(T-t)}S_t^\beta e^{(r\beta -\frac 12\sigma ^2\beta )(T-t)}\E ^\Q \l [e^{\sigma \beta (B_T-B_t)}\r ]\\ &=e^{-r(T-t)}S_t^\beta e^{(r\beta -\frac 12\sigma ^2\beta )(T-t)}e^{\frac 12\sigma ^2\beta ^2(T-t)}\\ &=S_t^\beta e^{-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )}. \end{align*} Here, we use that \(S_t\) is \(\mc {F}_t\) measurable. We then use (11.2) along with the properties of Brownian motion to tell us that \(\sigma \beta (B_T-B_t)\) is independent of \(\mc {F}_t\) with distribution \(N(0,\sigma ^2\beta ^2(T-t))\).

• 15.5 From Theorem 15.3.1 the price at time \(t\) of the binary option is

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} e^{-r(T-t)}\E ^\Q \l [\Phi (S_T)\|\mc {F}_t\r ] &=Ke^{-r(T-t)}\E ^\Q \l [\1_{\{S_T\in [\alpha ,\beta ]\}}\|\mc {F}_t\r ]\\ \end{align*} We have

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} S_T&=S_te^{(r-\frac 12\sigma ^2)(T-t)+\sigma (B_T-B_t)}\\ &=S_t e^{(r-\frac 12\sigma ^2)(T-t)+\sigma \sqrt {T-t} Z} \end{align*} where \(Z\sim N(0,1)\) is independent of \(\mc {F}_t\). Here we use that \(B_T-B_t\sim N(0,T-t)\sim \sqrt {T-t}N(0,1)\) is independent of \(\mc {F}_t\). Therefore,

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} \E ^\Q \l [\1_{\{S_T\in [\alpha ,\beta ]\}}\|\mc {F}_t\r ] &=\E ^\Q \l [\1_{\l \{S_t e^{(r-\frac 12\sigma ^2)(T-t)+\sigma \sqrt {T-t} Z}\in [\alpha ,\beta ]\r \}}\,\Big |\,\mc {F}_t\r ]\\ &=\E ^\Q \l [\1\l \{\frac {\log \l (\frac {\alpha }{S_t}\r )-\l (r+\frac 12\sigma ^2\r )(T-t)}{\sigma \sqrt {T-t}}\leq Z\leq \frac {\log \l (\frac {\beta }{S_t}\r )-\l (r+\frac 12\sigma ^2\r )t}{\sigma \sqrt {T-t}}\r \}\,\Bigg |\,\mc {F}_t\r ]\\ &=\E ^\Q \l [\1\l \{\frac {\log \l (\frac {\alpha }{S_t}\r )-\l (r+\frac 12\sigma ^2\r )(T-t)}{\sigma \sqrt {T-t}}\leq Z\leq \frac {\log \l (\frac {\beta }{S_t}\r )-\l (r+\frac 12\sigma ^2\r )t}{\sigma \sqrt {T-t}}\r \}\r ]\\ &=\mc {N}(e_2)-\mc {N}(e_1) \end{align*} where

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} e_1&=\frac {\log \l (\frac {\alpha }{S_t}\r )-\l (r+\frac 12\sigma ^2\r )(T-t)}{\sigma \sqrt {T-t}}\\ e_2&=\frac {\log \l (\frac {\beta }{S_t}\r )-\l (r+\frac 12\sigma ^2\r )(T-t)}{\sigma \sqrt {T-t}}. \end{align*} Hence the price at time \(t\) is given by \(Ke^{r(T-t)}\l [\mc {N}(e_1)-\mc {N}(e_2)\r ].\)

• 15.6 If we take \(F_t=e^{\mu t}\) then (in world \(\P \)) we have

  \[\frac {S_t}{F_t}=\frac {S_0\exp \l (\l (\mu -\tfrac 12\sigma ^2\r )t+\sigma B_t\r )}{\exp \l (\mu t\r )}=S_0\exp \l (\sigma B_t-\frac 12\sigma ^2 t\r ),\]

  which we showed was a martingale in 11.6.

• 15.7 We have the risk neutral pricing formula \(\Pi _t(\Phi )=e^{-r(T-t)}\E ^\Q _{t,S_t}[\Phi (S_T)]\) for any contingent claim \(\Phi \). Hence, using linearity of \(\E ^\Q \),

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} \Pi _t(\alpha \Phi _1+\beta \Phi _2) &=e^{-r(T-t)}\E ^\Q _{t,S_t}\l [\alpha \Phi _1(S_T)+\beta \Phi _2(S_T)\r ]\\ &=\alpha e^{-r(T-t)}\E ^\Q _{t,S_t}\l [\Phi _1(S_T)\r ]+\beta e^{-r(T-t)}\E ^\Q _{t,S_t}\l [\Phi _2(S_T)\r ]\\ &=\alpha \Pi _t(\Phi _1)+\beta \Pi _t(\Phi _2) \end{align*} as required.

• 15.8 In the ‘new’ model we could indeed buy a unit of \(Y_t=S_t^\beta \) and hold onto it for as long as we liked. But in the ‘old’ model we can only buy (linear multiples of) the stock \(S_t\); we can’t buy a commodity whose price at time \(t\) is \(S_t^\beta \). This means that the hedging strategy suggested within the ‘new’ model doesn’t work within the ‘old’ model. Consequently, there is no reason to expect that prices in the two models will be equal. In general they will not be.

Chapter 16

• 16.1

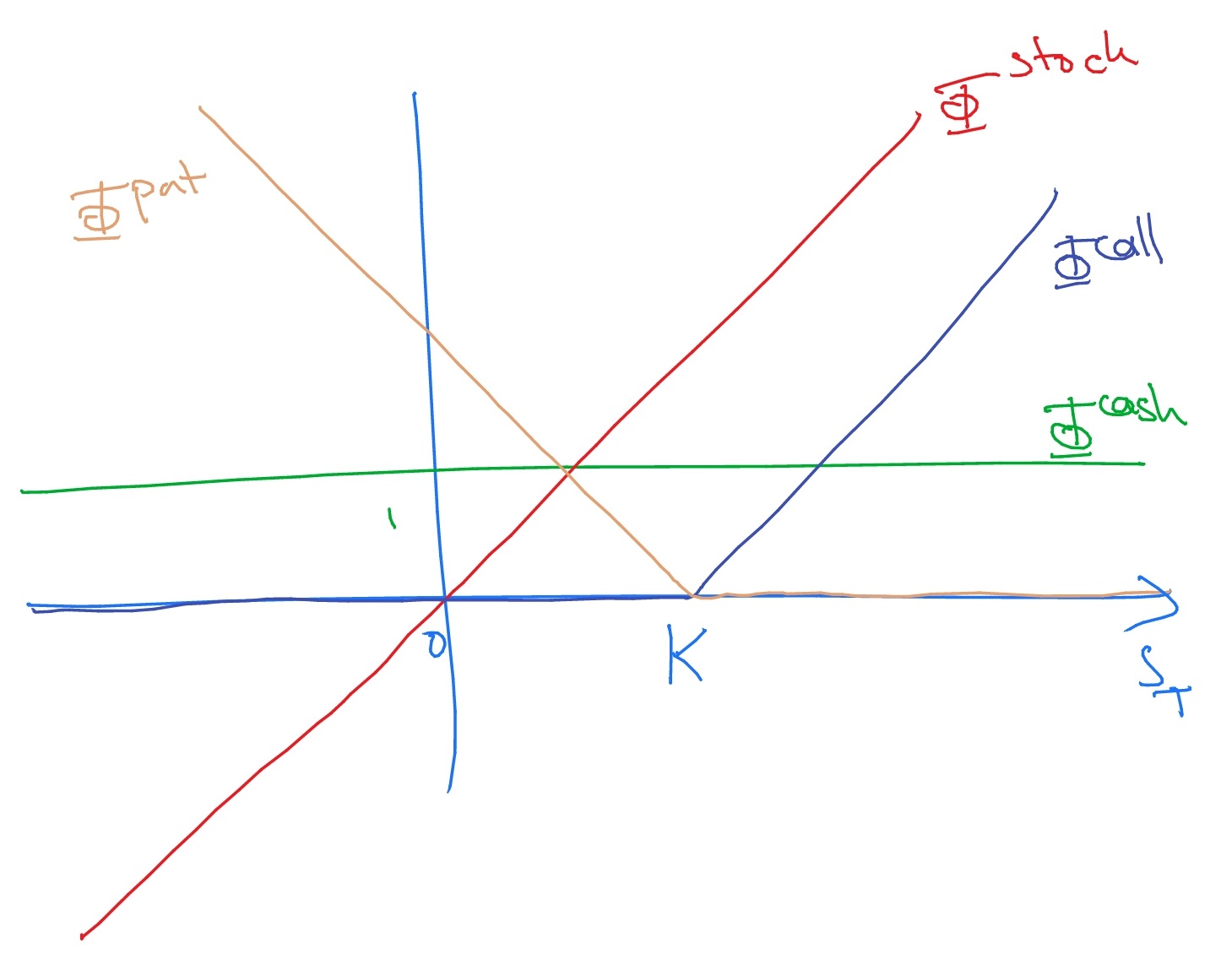
  • (a) The functions \(\Phi ^{cash}(S_T)=1\), \(\Phi ^{stock}(S_T)=S_T\), \(\Phi ^{call}(S_T)=\max (S_T-K,0)\) and \(\Phi ^{put}(S_T)=\max (K-S_T,0)\) look like:

    

  • (b) In terms of functions, the put-call parity relation states that

    \[\max (K-S_T,0)=\max (S_T-K)+K-S_T.\]

    To check that this holds we consider two cases.

    • • If \(K\leq S_T\) then put-call parity states that \(0=S_T-K+K-S_T\), which is true.

    • • If \(K\geq S_T\) then put-call parity states that \(K-S_T=0+K-S_T\), which is true.

• 16.2 The put-call parity relation (16.1) says that

  \[\Phi ^{put}(S_T)=\Phi ^{call}(S_T)+K\Phi ^{cash}(S_T) -\Phi ^{stock}(S_T).\]

  Hence,

  \[\Pi ^{put}_t=\Pi ^{call}_t+K\Pi ^{cash}_t-\Pi ^{stock}_t.\]

  From here, using that \(\Pi ^{cash}_t=e^{-r(T-t)}\) (corresponding to \(\Phi (S_T)=1\)) and \(\Pi ^{stock}_t=S_t\) (corresponding to \(\Phi (S_T)=S_T\)), as well as the Black-Scholes formula (15.23), we have

  \(\seteqnumber{0}{C.}{5}\)

  \begin{align*} \Pi ^{put}_t &=S_t\mc {N}[d_1]-Ke^{-r(T-t)}\mc {N}[d_2]+Ke^{-r(T-t)}-S_t\\ &=S_t(\mc {N}[d_1]-1)-Ke^{-r(T-t)}(\mc {N}[d_2]-1)\\ &=-S_t\mc {N}[-d_1]+Ke^{-r(T-t)}\mc {N}[-d_2]. \end{align*} In the last line we use that \(\mc {N}[x]+\mc {N}[-x]=1\), which follows from the fact that the \(N(0,1)\) distribution is symmetric about \(0\) (i.e. \(\P [X\leq x]+\P [X\leq -x]=\P [X\leq x]+\P [-X\geq x]=\P [X\leq x]+\P [X\geq x]=1\)). The formula stated in the question follows from setting \(t=0\).

• 16.3 Write \(\Phi ^{call,K}(S_T)=\max (S_T-K,0)\) for the contingent claim of a European call option, and \(\Phi ^{put,K}(S_T)\) for the contingent claim of a European put options, both with strike price \(K\) and exercise date \(T\). Then

  \[\Phi (S_T)=\Phi ^{call,1}(S_T)+\Phi ^{put,-1}(S_T)\]

  so we can hedge \(\Phi (S_T)\) by holding a single call option with strike price \(1\) and a single put option with strike price \(-1\).

• 16.4

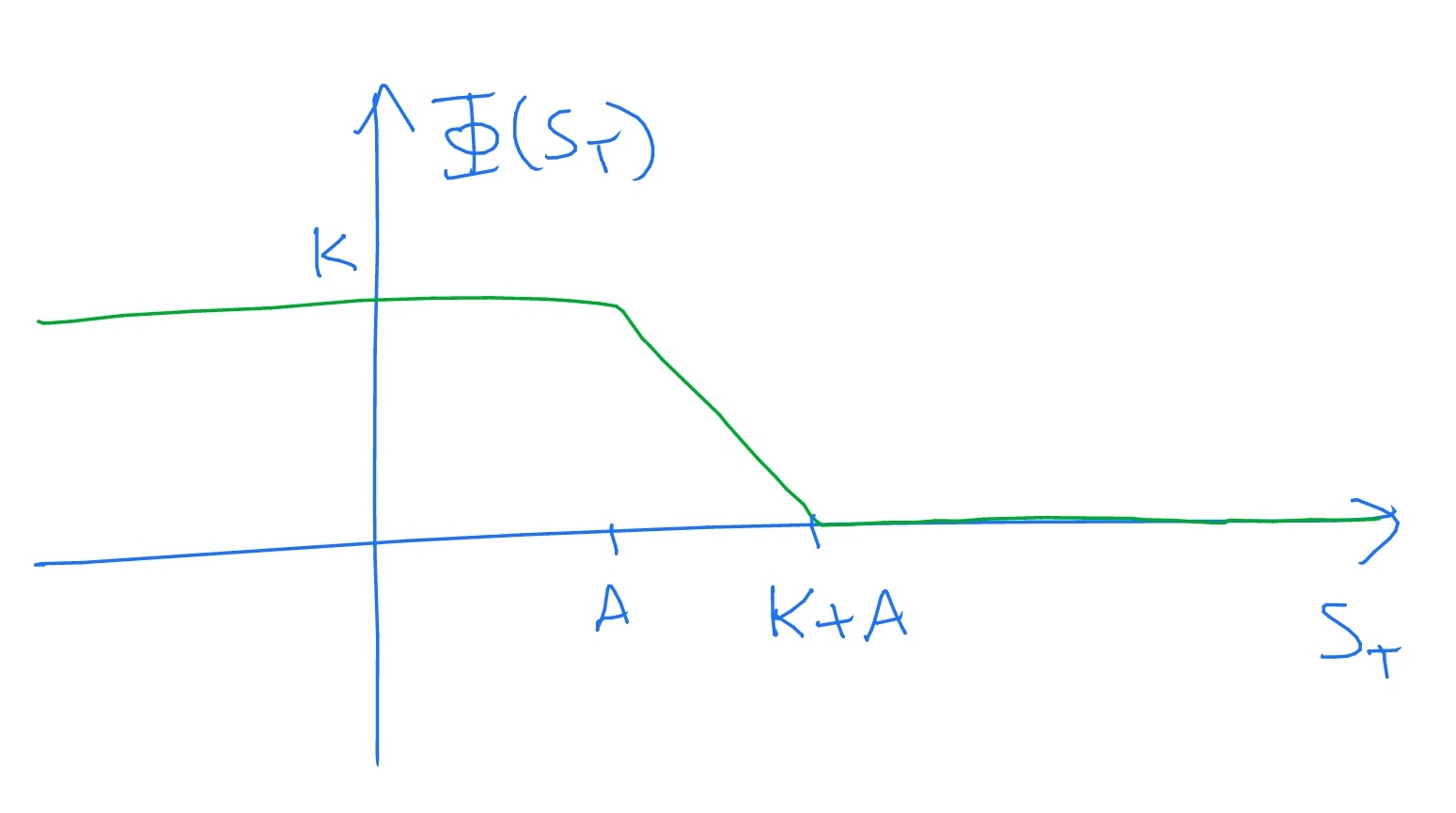
  • (a) A sketch of \(\Phi (S_T)\) for general \(A\) looks like

    

    Let \(\Phi ^{put,K}(S_T)=\max (K-S_T,0)\) denote the contingent claim corresponding to a European put option with strike price \(K\) and exercise date \(T\). Then, we claim that

    \(\seteqnumber{0}{C.}{5}\)

    \begin{equation} \label {eq:put-bull} \Phi (S_T)=\Phi ^{put,K+A}(S_T)-\Phi ^{put,A}(S_T). \end{equation}

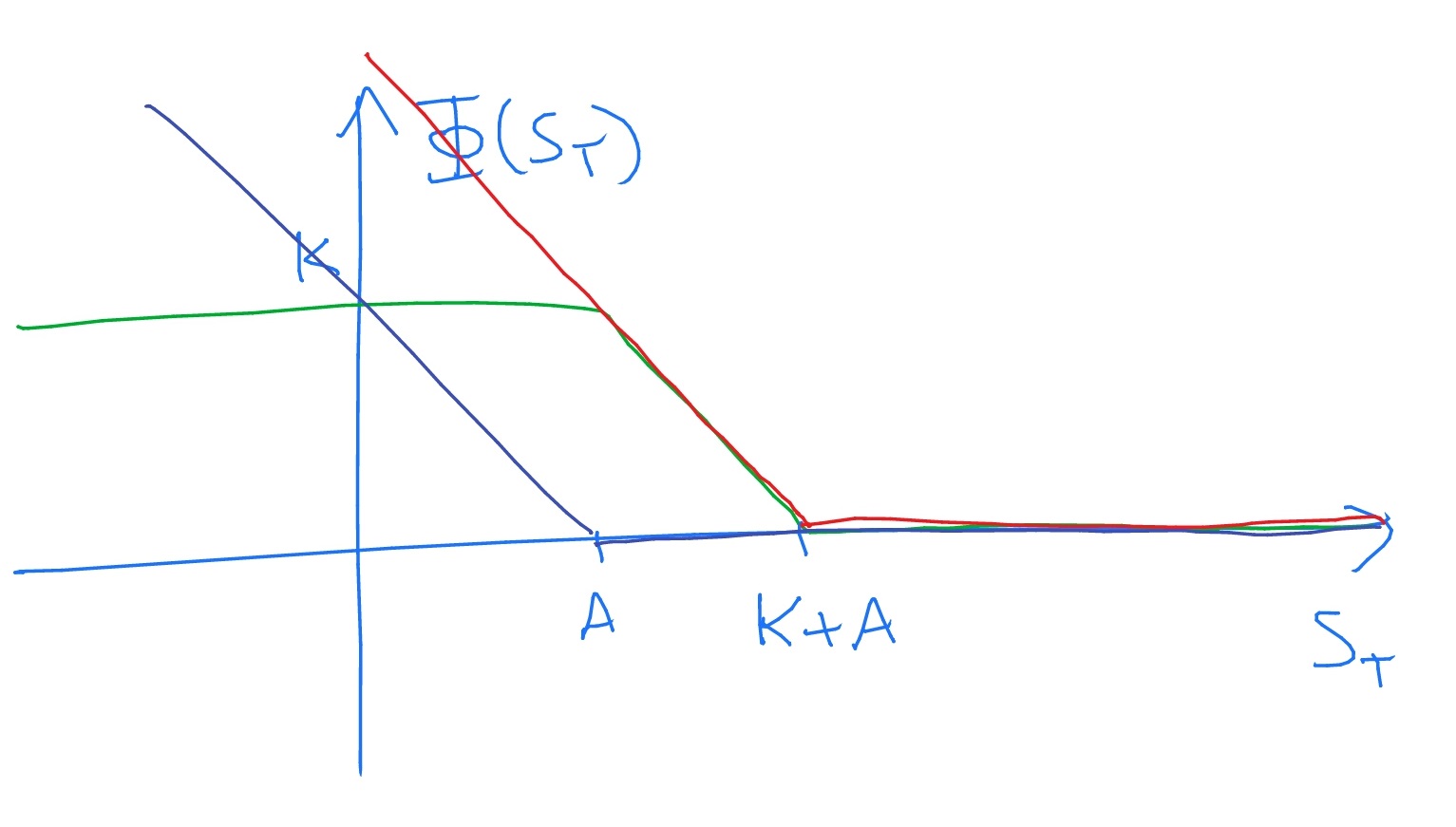
    The right-hand side of this equation corresponds to a portfolio of one put option with strike price \(K+A\) and minus one put option with strike price \(A\). We can see that the relation (C.6) holds by using a diagram

    

    in which the purple line \(\Phi ^{put,A}(S_T)\) is subtracted from the red line \(\Phi ^{put,K+A}(S_T)\) to obtain the green line \(\Phi (S_T)\). Alternatively, we can check it by considering three cases:

    • • If \(S_T\leq A\) then we have \(K=(K+A-S_T)-(A-S_T)\) which is true.

    • • If \(A\leq S_T\leq K+A\) then we have \(K+A-S_T=(K+A-S_T)-(0)\) which is true.

    • • If \(S_T\geq K+A\) then we have \(0=(0)-(0)\) which is true.

    Therefore, the portfolio of one put option with strike price \(K+A\) and minus one put option with strike price \(A\) is a replicating portfolio for \(\Phi (S_T)\).

  • (b) We use put-call parity to replicate our portfolio of put options with a portfolio of cash, stock and call options. This tells us that \(\Phi ^{put,K}(S_T)=\Phi ^{call,K}(S_T)+K\Phi ^{cash}(S_T)+\Phi ^{stock}(S_T)\). Therefore, replacing each of our put options with the equivalent amounts of cash and stock, we have

    \(\seteqnumber{0}{C.}{6}\)

    \begin{align*} \Phi ^{put,K+A}(S_T)-\Phi ^{put,A}(S_T) &=\Phi ^{call,K+A}(S_T)-\Phi ^{call,A}(S_T)+(K+A-A)\Phi ^{cash}(S_T)-(1-1)\Phi ^{stock}(S_T)\\ &=\Phi ^{call,K+A}(S_T)-\Phi ^{call,A}(S_T)+K\Phi ^{cash}(S_T). \end{align*} Hence, \(\Phi (S_T)\) can be replicated with a portfolio containing one call option with strike price \(K+A\), minus one call option with strike price \(K\), and \(K\) units of cash.

  • (c) Corollary 15.3.3 refers to portfolios consisting only of stocks and cash. It does not apply to portfolios that are also allowed to contain derivatives.

• 16.5 We can write

  \[\Phi ^{bull}(S_T)=A+\max (S_T-A,0)-\max (S_T-B,0).\]

  It may help to draw a picture, in the style of 16.4. If we write \(\Phi ^{call,K}(S_T)=\max (S_T-K,0)\) and recall that \(\Phi ^{cash}(S_T)=1\) then we have

  \[\Phi ^{bull}(S_T)=A\Phi ^{cash}(S_T)+\Phi ^{call,A}(S_T)-\Phi ^{call,B}(S_T).\]

  So, in our (constant) hedging portfolio at time \(0\) we will need \(Ae^{-rT}\) in cash, one call option with strike price \(A\), and minus one call option with strike price \(B\).

• 16.9 The price computed for the contingent claim \(\Phi (S_T)=S_t^\beta \) in 15.4 is

  \[F(t,S_t)=S_t^\beta \exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r ).\]

  (Recall that Theorem 15.3.1 also tells us that there is a hedging strategy \(h_t=(x_t,y_t)\) for the contingent claim with value \(F(t,S_t)\).)

  We have \(F(t,s)=s^\beta \exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r )\) and we calculate

  \(\seteqnumber{0}{C.}{6}\)

  \begin{align*} \Delta _F&=\frac {\p F}{\p s}(t,S_t)=\beta S_t^{\beta -1}\exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r )\\ \Gamma _F&=\frac {\p ^2 F}{\p s^2}(t,S_t)=\beta (\beta -1) S_t^{\beta -2}\exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r )\\ \Theta _F&=\frac {\p F}{\p t}(t,S_t)=S_t^\beta (1-\beta )(r+\tfrac 12\beta \sigma ^2)\exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r )\\ \rho _F&=\frac {\p F}{\p r}(t,S_t)=-S_t^\beta (T-t)(1-\beta )\exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r )\\ \mc {V}_F&=\frac {\p F}{\p \sigma }(t,S_t)=-S_t^\beta \sigma \beta (T-t)(1-\beta )\exp \l (-r(T-t)(1-\beta )-\frac 12\sigma ^2\beta (T-t)(1-\beta )\r ). \end{align*}

• 16.10

  • (a) The underlying stock \(S_t\) has \(\Delta _S=1\) and \(\Gamma _S=0\). If we add \(-2\) stock into our original portfolio with value \(F\), then its new value is \(V(t,S_t)=F(t,S_t)-2S_t\), which satisfies \(\Delta _V=\Delta _F-2=0\).

    The cost of adding \(-2\) units of stock into the portfolio is \(-2S_t\).

  • (b) After including an amount \(w_t\) of stock and an amount \(d_t\) of \(D\), we have

    \[V(t,S_t)=F(t,S_t)+w_tS_t+d_tD(t,S_t).\]

    Hence, we require that

    \(\seteqnumber{0}{C.}{6}\)

    \begin{align*} 0&=\Delta _F+w_t+d_t\Delta _D=2+w_t+d_t,\\ 0&=\Gamma _F+d_t\Gamma _D=3+2d_t. \end{align*} The solution is \(d_t=\frac {-3}{2}\) and \(w_t=\frac {-1}{2}\).

    The cost of the extra stock and units of \(D\) that we have had to include is \(-\frac 32D(t,S_t)-\frac 12S_t\).

• 16.11

  • (a) It doesn’t work because adding in an amount \(z_t\) of \(Z\) in the second step will (typically i.e. if \(\Delta _Z\neq 0\)) destroy the delta neutrality that we gained from the first step.

  • (b) Since \(Z(t,S_t)=S_t\) we have

    \[V(t,S_t)=F(t,S_t)+w_tW(t,S_t)+z_tS_t,\]

    so we require that

    \(\seteqnumber{0}{C.}{6}\)

    \begin{align*} 0&=\frac {\p V}{\p s}=\Delta _F+w_t\Delta _{W}+z_t\\ 0&=\frac {\p ^2 V}{\p s^2}=\Gamma _F+w_t\Gamma _{W}. \end{align*} The solution is easily seen to be

    \(\seteqnumber{0}{C.}{6}\)

    \begin{align*} w_t&=-\frac {\Gamma _{F}}{\Gamma _{W}}\\ z_t&=\frac {\Delta _{W}\Gamma _F}{\Gamma _{W}}-\Delta _F \end{align*}

  • (c) This idea works. As we can see from part (b), if we use stock as our financial derivative \(Z(t,S_t)=S_t\), then \(\Gamma _Z=0\). Hence, adding in a suitable amount of stock in the second step can achieve delta neutrality without destroying the gamma neutrality obtained in the first step.

• 16.12 Omitted (good luck).

Chapter 19

• 19.1 The degrees of the nodes, in alphabetical order, are \((1,1), (0,2), (2,2), (2,0), (1,1), (1,2), (1,0).\) This gives a degree distribution

  \[ \P [D_G=(a,b)]= \begin {cases} \frac 17 & \text { for }(a,b)\in \{(0,2), (2,2), (2,0), (1,2), (1,0)\},\\ \frac 27 & \text { for }(a,b)=(1,1). \end {cases} \]

  Sampling a uniformly random and moving along it means that the chance of ending up at a node \(A\) is proportional to \(\indeg (A)\). Since the graph has \(8\) edges, we obtain

  \(\seteqnumber{0}{C.}{6}\)

  \begin{align*} \P [O=n] &= \begin{cases} \frac 18+\frac 28 & \text { for }n=0\text { (nodes D and G)}\\ \frac 18+\frac 18 & \text { for }n=1\text { (nodes A and E)}\\ 0+\frac 28+\frac 18 & \text { for }n=2\text { (nodes B,C and F)} \end {cases}\\ &= \begin{cases} \frac 38 & \text { for }n=0\\ \frac 14 & \text { for }n=1\\ \frac 38 & \text { for }n=2 \end {cases} \end{align*}

• 19.2 Node \(Y\) can fail only if the cascade of defaults includes \(X\to D \to Y\). Given that \(X\) fails, the probability that \(X\) fails is \(\eta _3=\frac 13\), because \(D\) has \(3\) in-edges. Similarly, given that \(D\) fails, the probability that \(Y\) also fails is \(\frac 12\). Hence, the probability that \(Y\) fails, given that \(X\) fails, is \(\frac 16\).

• 19.3 Node \(Y\) can fail if the cascade of defaults includes \(X\to B\to D \to Y\) or \(X\to B \to C\to D\to Y\). Given that \(X\) fails, node \(B\) is certain to fail as well, since \(B\) has only one in-edge. Given that \(B\) fails, \(C\) is certain to fail for the same reason. Therefore, the edges \((B,D)\) and \((C,D)\) are both certain to default. For each of these edges, independently, there is a chance \(\frac 13\) that their own default causes \(D\) to fail. The probability that \(D\) fails is therefore

  \[\frac 13+\l (1-\frac 13\r )\times \frac 13=\frac 59.\]

  Here, we condition first on if the link \(BD\) causes \(D\) to fail (which it does with probability \(\frac 13\)) and then, if it doesn’t (which has probability \(1-\frac 13\)) we ask if the link \(BC\), which fails automatically and causes failure of \(CD\), causes \(D\) to fail.

  Given that \(D\) fails, \(Y\) is certain to fail. Hence, the probability that \(Y\) fails, given that \(X\) fails, is \(\frac 59\).

• 19.4 For any node of the graph (except for the root node), if its single incoming loan defaults, then its own probability of default if \(\alpha \), independently of all else. Hence, each newly defaulted loan leads to two further defaulted loans with probability \(\alpha \), and leads to no further defaulted loans with probability \(1-\alpha \). Hence, the defaulted loans form a Galton-Watson process \((Z_n)\) with off-spring distribution \(G\), given by \(\P [G=2]=\alpha \) and \(\P [G=0]=1-\alpha \), with initial state \(Z_0=2\) (representing the two loans which initially default when \(V_0\) defaults).

  The total number of defaulted edges is given by

  \[S=\sum \limits _{n=0}^\infty Z_n.\]

  Combining Lemmas 7.4.7, 7.4.6 and 7.4.8, we know that either:

  • • If \(\E [G]>1\) then there is positive probability that \(Z_n\to \infty \) as \(n\to \infty \); in this case for all large enough \(n\) we have \(Z_n\geq 1\), and hence \(S=\infty \).

  • • If \(\E [G]\leq 1\) then, almost surely, for all large enough \(n\) we have \(Z_n=0\), which means that \(S<\infty \).

  We have \(\E [G]=2\alpha \). It is clear that the number of defaulted banks is infinite if and only if the number of defaulted loans in infinite, which has positive probability if \(\E [G]>1\). So, we conclude that there is positive probability of a catastrophic default if and only if \(\alpha >\frac 12\).

• 19.5

  • (a) The probability that both \(B\) and \(C\) fail is \(\frac 12\frac 12=\frac 14\). Given this event, the probability that both \(D\) and \(E\) fail is \(\frac 12(1-\frac 34\frac 34\frac 34)=\frac {37}{128}\); here the first term \(\frac 12\) is the probability of \(D\) failing (via its link to \(B\)) and the second term is one minus the probability of \(E\) not failing despite all its inbound loans defaulting. Given that \(D\) and \(E\) both fail, the probability that \(F\) fails is \(1-\frac 23\frac 23=\frac 59\).

    Hence, the probability that every node fails is

    \[\frac 14\frac {37}{128}\frac 59=\frac {185}{4608}.\]

  • (b) Our strategy comes in three stages: first work out the probabilities of all the possible outcomes relating to \(B\) and \(C\); secondly, do the same for \(D\) and \(E\); finally, do the same for \(F\). Each stage relies on the information obtained in the previous stage.

    Stage 1: The probability that \(B\) fails and \(C\) does not is \(\frac 12\frac 12=\frac 14\). This is also the probability that \(C\) fails and \(B\) does not. The probability that both \(B\) and \(C\) fail is also \(\frac 14\).

    Stage 2: Hence, the probability that \(E\) fails and \(D\) does not is

    \[\frac 14\l (\frac 14\frac 12\r )+\frac 14\l (\frac 14\r )+\frac 14\l (\frac 12\r )\l (\frac 14+\frac 34\frac 14\r )=\frac {19}{128}\]

    The three terms in the above correspond respectively to the three cases considered in the first paragraph. Similarly, the probability that \(D\) fails and \(E\) does not is

    \[\frac 14\l (\frac 12\frac 34\frac 34\r )+\frac 14\l (0\r )+\frac 14\l (\frac 12\r )\l (\frac 34\frac 34\frac 34\r )=\frac {63}{512}\]

    and the probability that both \(D\) and \(E\) fail is

    \[\frac 14\l (\frac 12\r )\l (\frac 14+\frac 34\frac 14\r )+\frac 14\l (0\r )+\frac 14\l (\frac 12\r )\l (1-\frac 34\frac 34\frac 34\r )=\frac {65}{512}\]

    .

    Stage 3: Finally, considering these three cases in turn, the probability that \(F\) fails is

    \[\frac {19}{128}\l (\frac 13\r )+\frac {63}{512}\l (\frac 13\r )+\frac {65}{512}\l (1-\frac 23\frac 23\r )=\frac {371}{2304}.\]