Stochastic Processes and Financial Mathematics
(part one)

5.2 Hedging in the one-period model

We saw in Section 1.3 that the ‘no arbitrage’ assumption could force some prices to take particular values. It is not immediately obvious if the absence of arbitrage forces a unique value for every price; we will show in this section that it does.

First, let us write down exactly what it is that we need to price.

Definition 5.2.1 A contingent claim is any random variable of the form $X = Φ (S_{1})$ , where $Φ$ is a deterministic function.

The function $Φ$ is sometimes known as the contract function. One example of a contingent claim is a forward contract, in which the holder promises to buy a unit of stock at time $1$ for a fixed price $K$ , known as the strike price. In this case the contingent claim would be

$Φ (S_{1}) = S_{1} - K,$

the value of a unit of stock at time $1$ minus the price paid for it. We will see many other examples in the course. Here is another.

Example 5.2.2 A European call option gives its holder the right (but not the obligation) to buy, at time $1$ , a single unit of stock for a fixed price $K$ that is agreed at time $0$ . As for futures, $K$ is known as the strike price.

Suppose we hold a European call option at time $1$ . Then, if $S_{1} > K$ , we could exercise our right to buy a unit of stock at price $K$ , immediately sell the stock for $S_{1}$ and consequently earn $S_{1} - K > 0$ in cash. Alternatively if $S_{1} \leq K$ then our option is worthless.

Since $S_{1}$ is equal to either to either $s u$ or $s d$ , the only interesting case is when $s d < K < s u$ . In this case, the contingent claim for our European call option is

$\begin{matrix} (5.5) & Φ (S_{1}) = {\begin{cases} s u - K & if S_{1} = s u \\ 0 & if S_{1} = s d . \end{cases} \end{matrix}$

In the first case our right to buy is worth exercising; in the second case it is not. A simpler way to write this contingent claim is

$\begin{matrix} (5.6) & Φ (S_{1}) = max (S_{1} - K, 0) . \end{matrix}$

In general, given any contract, we can work out its contingent claim. We therefore plan to find a general way of pricing contingent claims. In Section 1.3 we relied on finding specific trading strategies to determine prices (one, from the point of view of the buyer, that gave an upper bound and one, from the point of view of the seller, to give a lower bound). Our first step in this section is to find a general way of constructing trading strategies.

Definition 5.2.3 We say that a portfolio $h$ is a replicating portfolio or hedging portfolio for the contingent claim $Φ (S_{1})$ if $V_{1}^{h} = Φ (S_{1})$ .

The process of finding a replicating portfolio is known simply as replicating or hedging. The above definition means that, if we hold the portfolio $h$ at time $0$ , then at time $1$ it will have precisely the same value as the contingent claim $Φ (S_{1})$ . Therefore, since we assume our model is free of arbitrage:

If a contingent claim $Φ (S_{1})$ has a replicating portfolio $h$ , then the price of the $Φ (S_{1})$ at time $0$ must be equal to the value of $h$ at time $0$ .

We say that a market is complete if every contingent claim can be replicated. Therefore, if the market is complete, we can price any contingent claim.

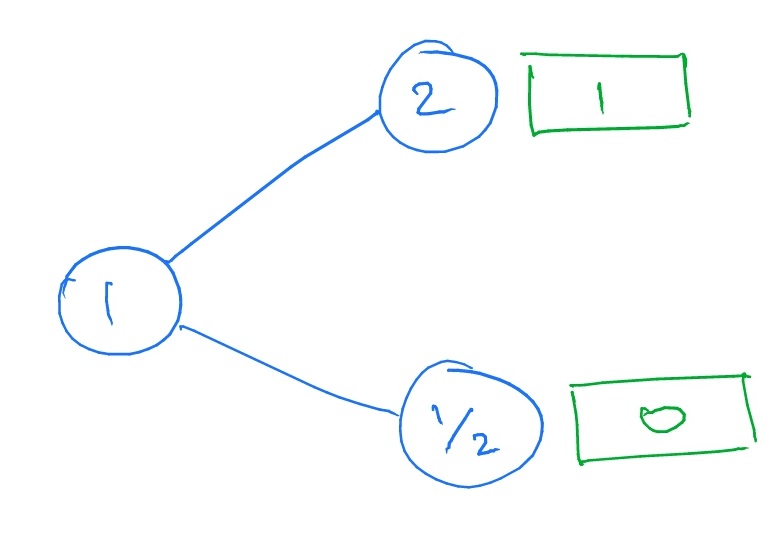
Example 5.2.4 Suppose that $s = 1, d = \frac{1}{2}, u = 2$ and $r = \frac{1}{4}$ , and that we are looking at the contingent claim

$Φ (S_{1}) = {\begin{cases} 1 & if S_{1} = s u, \\ 0 & if S_{1} = s d . \end{cases}$

We can represent this situation as a tree, with a branch for each possible movement of the stock, and the resulting value of our contingent claim written in a square box.

Suppose that we wish to replicate $Φ (S_{1})$ . That is, we need a portfolio $h = (x, y)$ such that $V_{1}^{h} = Φ (S_{1})$ :

$\begin{aligned} (1 + \frac{1}{4}) x + 2 y & = 1 \\ (1 + \frac{1}{4}) x + \frac{1}{2} y & = 0. \end{aligned}$ This is a pair of linear equations that we can solve. The solution (which is left for you to check) is $x = \frac{- 4}{15}$ , $y = \frac{2}{3}$ . Hence the price of our contingent claim $Φ (S_{1})$ at time $0$ is $V_{0}^{h} = \frac{- 4}{15} + 1 \cdot \frac{2}{3} = \frac{2}{5}$ .

Let us now take an arbitrary contingent claim $Φ (S_{1})$ and see if we can replicate it. This would mean finding a portfolio $h$ such that the value $V_{1}^{h}$ of the portfolio at time $1$ is $Φ (S_{1})$ :

$V_{1}^{h} = {\begin{cases} Φ (s u) & if S_{1} = s u, \\ Φ (s d) & if S_{1} = s d . \end{cases}$

By (5.1), if we write $h = (x, y)$ then we need

$\begin{aligned} (1 + r) x + s u y & = Φ (s u) \\ (1 + r) x + s d y & = Φ (s d), \end{aligned}$ which is just a pair of linear equations to solve for $(x, y)$ . In matrix form,

$\begin{matrix} (5.7) & (\begin{matrix} 1 + r & s u \\ 1 + r & s d \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} Φ (s u) \\ Φ (s d) \end{matrix}) . \end{matrix}$

A unique solution exists when the determinant is non-zero, that is when $(1 + r) s u - (1 + r) s d \neq 0$ , or equivalently when $u \neq d$ . So, in this case, we can find a replicating portfolio for any contingent claim.

It is an assumption of the model that $d \leq u$ , so we have that our one-period model is complete if $d < u$ . Therefore:

Proposition 5.2.5 If the one-period model is arbitrage free then it is complete.

And, in this case, we can solve (5.7) to get

$\begin{aligned} x & = \frac{1}{1 + r} \frac{u Φ (s d) - d Φ (s u)}{u - d}, \\ (5.8) & y & = \frac{1}{s} \frac{Φ (s u) - Φ (s d)}{u - d} . \end{aligned}$ which tells us that the price of $Φ (S_{1})$ at time $0$ should be

$\begin{aligned} V_{0}^{h} & = x + s y \\ = \frac{1}{1 + r} (\frac{(1 + r) - d}{u - d} Φ (s u) + \frac{u - (1 + r)}{u - d} Φ (s d)) \\ = \frac{1}{1 + r} (q_{u} Φ (s u) + q_{d} Φ (s d)) \\ = \frac{1}{1 + r} E^{Q} [Φ (S_{1})] . \end{aligned}$ Hence, the value (and therefore, the price) of $Φ (S_{1})$ at time $0$ , is given by

$\begin{matrix} (5.9) & V_{0}^{h} = \frac{1}{1 + r} E^{Q} [Φ (S_{1})] . \end{matrix}$

The formula (5.9) is known as the risk-neutral valuation formula. It says that to find the price of $Φ (S_{1})$ at time $0$ we should take its expectation according to $Q$ , and then discount one time step worth of interest i.e. divide by $1 + r$ . It is a very powerful tool, since it allows us to price any contingent claim.

Note the similarity of (5.9) to (5.4). In fact, (5.4) is a special case of (5.9), namely the case where $Φ (S_{1}) = S_{1}$ i.e. pricing the contingent claim corresponding to being given a single unit of stock.

To sum up:

Proposition 5.2.6 Let $Φ (S_{1})$ be a contingent claim. Then the (unique) replicating portfolio $h = (x, y)$ for $Φ (S_{1})$ can be found by solving $V_{1}^{h} = Φ (S_{1})$ , which can be written as a pair of linear equations:

$\begin{aligned} (1 + r) x + s u y & = Φ (s u) \\ (1 + r) x + s d y & = Φ (s d) . \end{aligned}$ The general solution is (5.8). The value (and hence, the price) of $Φ (S_{1})$ at time $0$ is

$V_{0}^{h} = \frac{1}{1 + r} E^{Q} [Φ (S_{1})] .$

For example, we can now both price and hedge the European call option.

Example 5.2.7 In (5.5) we found the contingent claim of a European call option with strike price $K \in (s d, s u)$ to be $Φ (S_{T}) = max (S_{T} - K, 0)$ . By the first part of Proposition 5.2.6, to find a replicating portfolio $h = (x, y)$ we must solve $V_{1}^{h} = Φ (S_{1})$ , which is

$\begin{aligned} (1 + r) x + s u y & = s u - K \\ (1 + r) x + s d y & = 0. \end{aligned}$ This has the solution (again, left for you to check) $x = \frac{s d (K - s u)}{(1 + r) (s u - s d)}, y = \frac{s u - K}{s u - s d}$ . By the second part of Proposition 5.2.6 the value of the European call option at time $0$ is

$\begin{aligned} \frac{1}{1 + r} E^{Q} [Φ (S_{1})] & = \frac{1}{1 + r} (q_{u} (s u - K) + q_{d} (0)) \\ = \frac{1}{1 + r} \frac{(1 + r) - d}{u - d} (s u - K) . \end{aligned}$

Stochastic Processes and Financial Mathematics (part one)

5.2 Hedging in the one-period model

Stochastic Processes and Financial Mathematics
(part one)