Bayesian Statistics

$\newcommand{\footnotename}{footnote}$ $\def \LWRfootnote {1}$ $\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\let \LWRorighspace \hspace $ $\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }$ $\newcommand {\mathnormal }[1]{{#1}}$ $\newcommand \ensuremath [1]{#1}$ $\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } $ $\newcommand {\setlength }[2]{}$ $\newcommand {\addtolength }[2]{}$ $\newcommand {\setcounter }[2]{}$ $\newcommand {\addtocounter }[2]{}$ $\newcommand {\arabic }[1]{}$ $\newcommand {\number }[1]{}$ $\newcommand {\noalign }[1]{\text {#1}\notag \\}$ $\newcommand {\cline }[1]{}$ $\newcommand {\directlua }[1]{\text {(directlua)}}$ $\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}$ $\newcommand {\protect }{}$ $\def \LWRabsorbnumber #1 {}$ $\def \LWRabsorbquotenumber "#1 {}$ $\newcommand {\LWRabsorboption }[1][]{}$ $\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }$ $\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }$ $\def \mathcode #1={\mathchar }$ $\let \delcode \mathcode $ $\let \delimiter \mathchar $ $\def \oe {\unicode {x0153}}$ $\def \OE {\unicode {x0152}}$ $\def \ae {\unicode {x00E6}}$ $\def \AE {\unicode {x00C6}}$ $\def \aa {\unicode {x00E5}}$ $\def \AA {\unicode {x00C5}}$ $\def \o {\unicode {x00F8}}$ $\def \O {\unicode {x00D8}}$ $\def \l {\unicode {x0142}}$ $\def \L {\unicode {x0141}}$ $\def \ss {\unicode {x00DF}}$ $\def \SS {\unicode {x1E9E}}$ $\def \dag {\unicode {x2020}}$ $\def \ddag {\unicode {x2021}}$ $\def \P {\unicode {x00B6}}$ $\def \copyright {\unicode {x00A9}}$ $\def \pounds {\unicode {x00A3}}$ $\let \LWRref \ref $ $\renewcommand {\ref }{\ifstar \LWRref \LWRref }$ $ \newcommand {\multicolumn }[3]{#3}$ $\require {textcomp}$ $\newcommand {\intertext }[1]{\text {#1}\notag \\}$ $\let \Hat \hat $ $\let \Check \check $ $\let \Tilde \tilde $ $\let \Acute \acute $ $\let \Grave \grave $ $\let \Dot \dot $ $\let \Ddot \ddot $ $\let \Breve \breve $ $\let \Bar \bar $ $\let \Vec \vec $ $\require {colortbl}$ $\let \LWRorigcolumncolor \columncolor $ $\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigrowcolor \rowcolor $ $\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigcellcolor \cellcolor $ $\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }$ $\require {mathtools}$ $\newenvironment {crampedsubarray}[1]{}{}$ $\newcommand {\smashoperator }[2][]{#2\limits }$ $\newcommand {\SwapAboveDisplaySkip }{}$ $\newcommand {\LaTeXunderbrace }[1]{\underbrace {#1}}$ $\newcommand {\LaTeXoverbrace }[1]{\overbrace {#1}}$ $\newcommand {\LWRmultlined }[1][]{\begin {multline*}}$ $\newenvironment {multlined}[1][]{\LWRmultlined }{\end {multline*}}$ $\let \LWRorigshoveleft \shoveleft $ $\renewcommand {\shoveleft }[1][]{\LWRorigshoveleft }$ $\let \LWRorigshoveright \shoveright $ $\renewcommand {\shoveright }[1][]{\LWRorigshoveright }$ $\newcommand {\shortintertext }[1]{\text {#1}\notag \\}$ $\newcommand {\vcentcolon }{\mathrel {\unicode {x2236}}}$ $\renewcommand {\intertext }[2][]{\text {#2}\notag \\}$ $\newenvironment {fleqn}[1][]{}{}$ $\newenvironment {ceqn}{}{}$ $\newenvironment {darray}[2][c]{\begin {array}[#1]{#2}}{\end {array}}$ $\newcommand {\dmulticolumn }[3]{#3}$ $\newcommand {\LWRnrnostar }[1][0.5ex]{\\[#1]}$ $\newcommand {\nr }{\ifstar \LWRnrnostar \LWRnrnostar }$ $\newcommand {\mrel }[1]{\begin {aligned}#1\end {aligned}}$ $\newcommand {\underrel }[2]{\underset {#2}{#1}}$ $\newcommand {\medmath }[1]{#1}$ $\newcommand {\medop }[1]{#1}$ $\newcommand {\medint }[1]{#1}$ $\newcommand {\medintcorr }[1]{#1}$ $\newcommand {\mfrac }[2]{\frac {#1}{#2}}$ $\newcommand {\mbinom }[2]{\binom {#1}{#2}}$ $\newenvironment {mmatrix}{\begin {matrix}}{\end {matrix}}$ $\newcommand {\displaybreak }[1][]{}$ $ \def \offsyl {(\oslash )} \def \msconly {(\Delta )} $ $ \DeclareMathOperator {\var }{var} \DeclareMathOperator {\cov }{cov} \DeclareMathOperator {\Bin }{Bin} \DeclareMathOperator {\Geo }{Geometric} \DeclareMathOperator {\Beta }{Beta} \DeclareMathOperator {\Unif }{Uniform} \DeclareMathOperator {\Gam }{Gamma} \DeclareMathOperator {\Normal }{N} \DeclareMathOperator {\Exp }{Exp} \DeclareMathOperator {\Cauchy }{Cauchy} \DeclareMathOperator {\Bern }{Bernoulli} \DeclareMathOperator {\Poisson }{Poisson} \DeclareMathOperator {\Weibull }{Weibull} \DeclareMathOperator {\IGam }{IGamma} \DeclareMathOperator {\NGam }{NGamma} \DeclareMathOperator {\ChiSquared }{ChiSquared} \DeclareMathOperator {\Pareto }{Pareto} \DeclareMathOperator {\NBin }{NegBin} \DeclareMathOperator {\Studentt }{Student-t} \DeclareMathOperator *{\argmax }{arg\,max} \DeclareMathOperator *{\argmin }{arg\,min} $ \( \def \to {\rightarrow } \def \iff {\Leftrightarrow } \def \ra {\Rightarrow } \def \sw {\subseteq } \def \mc {\mathcal } \def \mb {\mathbb } \def \sc {\setminus } \def \wt {\widetilde } \def \v {\textbf } \def \E {\mb {E}} \def \P {\mb {P}} \def \R {\mb {R}} \def \C {\mb {C}} \def \N {\mb {N}} \def \Q {\mb {Q}} \def \Z {\mb {Z}} \def \B {\mb {B}} \def \~{\sim } \def \-{\,;\,} \def \qed {$\blacksquare $} \CustomizeMathJax {\def \1{\unicode {x1D7D9}}} \def \cadlag {c\`{a}dl\`{a}g} \def \p {\partial } \def \l {\left } \def \r {\right } \def \Om {\Omega } \def \om {\omega } \def \eps {\epsilon } \def \de {\delta } \def \ov {\overline } \def \sr {\stackrel } \def \Lp {\mc {L}^p} \def \Lq {\mc {L}^p} \def \Lone {\mc {L}^1} \def \Ltwo {\mc {L}^2} \def \toae {\sr {\rm a.e.}{\to }} \def \toas {\sr {\rm a.s.}{\to }} \def \top {\sr {\mb {\P }}{\to }} \def \tod {\sr {\rm d}{\to }} \def \toLp {\sr {\Lp }{\to }} \def \toLq {\sr {\Lq }{\to }} \def \eqae {\sr {\rm a.e.}{=}} \def \eqas {\sr {\rm a.s.}{=}} \def \eqd {\sr {\rm d}{=}} \def \approxd {\sr {\rm d}{\approx }} \def \Sa {(S1)\xspace } \def \Sb {(S2)\xspace } \def \Sc {(S3)\xspace } \)

Chapter 2 Discrete Bayesian models

A model is a machine for simulating data. We hope that the data we simulate is a realistic, or approximately realistic, copy of some part of the real world. In probability and statistics we use random models, meaning that if we use the same model twice we won’t generate the same data.

The reason for using a random model is that we can express our level of certainty. We don’t know exactly what will happen, so instead we create a model that includes a range of possibilities, along with a description how likely these different possibilities are. If we have a high level of certainty then we might choose a model in which the likely outcomes are very similar to each other. If not, we might choose a model in which the likely outcomes span a wide range of possibilities.

We usually allow our models to have parameters. Parameters are ‘input’ values that we can use to control how a model behaves, and we try to choose them in a way that makes our model best reflect reality.

2.1 Models with random parameters

We are often confident in our choice of model, but we are almost never certain what the best choice of parameters is. In that situation, we usually do have some degree of confidence in which parameter values should be used. How should we communicate that information? One way is to use random variables for the parameters, as we did in Section 1.7. If we have a high level of certainty in which parameter values should be used, then we will choose a random variable in which the likely outcomes are all very similar parameter values. If not then we choose a random variable in which the likely outcomes span a wide range of different parameters. The ‘parameters’ become just another part of the random model.

Example 2.1.1 We want to model the random number $X$ of successful experiments, out of a sequence of $10$ independent experiments, where each experiment has the same probability $p\in [0,1]$ of success. A natural form for $X$ is $\Bin (10,p)$, but we don’t know the value of $p$, so let us set $M_p\sim \Bin (10,p)$. Then $(M_p)$ is a family of distributions. We hope that one of these distributions will be a good model.

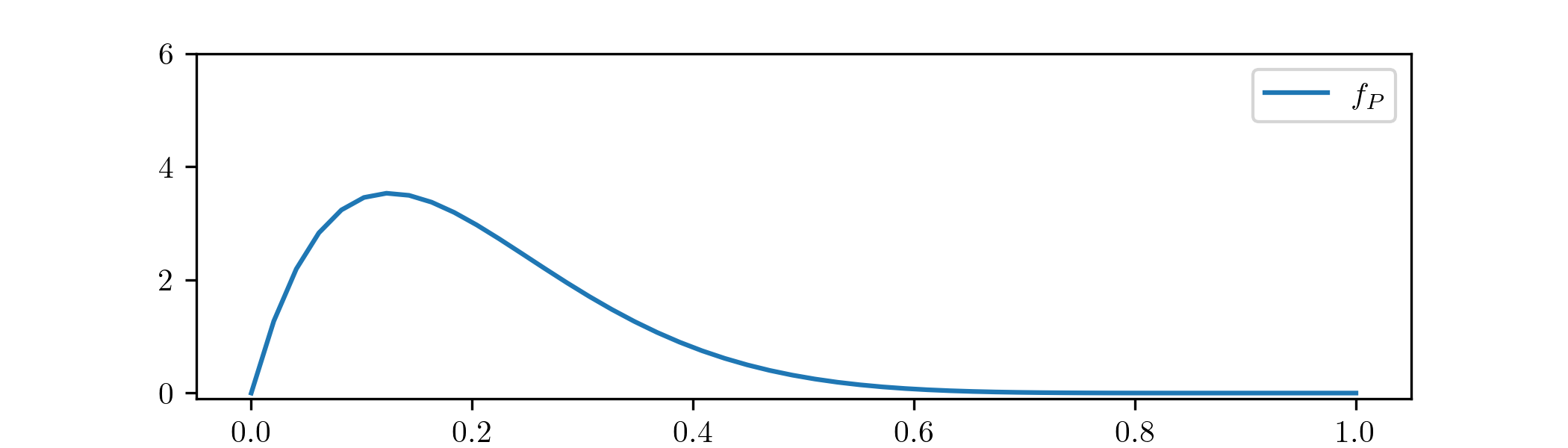
We are told (by a scientist colleague, say) that a reasonable estimate for $p$ is $p\approx \frac 15$, but they don’t seem very confident and for now that is all we know. We decide that our model for $p$ will be a random variable $P\sim \Beta (2,8)$, which has $\E [P]=\frac 15$ and probability density function
$\seteqnumber{0}{2.}{0}$
\begin{equation} \label {eq:beta28_pdf} f_P(p)=\begin{cases} 72p(1-p)^7\,dp & \text { for }p\in [0,1] \\ 0 & \text { otherwise.} \end {cases} \end{equation}

The decision here to use $\Beta (2,8)$ is a bit arbitrary – we will spend a large part of this course thinking about how to make such choices well! It is only meant here as example of the type of model that we will be interested in. We have chosen a distribution with range $[0,1]$, which is the set of possible values for $p$, and with most of its mass within the region $p\approx \frac 15$ that was suggested to us.

The random variable $(X,P)$ that results from this procedure is precisely the type we studied in Section 1.7. We want $X|_{\{P=p\}}\sim \Bin (10,p)$ and (for now) our best guess for the parameter is $P\sim \Beta (2,8)$. From Section 1.7 we know that the model we want is
$\seteqnumber{0}{2.}{1}$
\begin{equation} \label {eq:baby_bayes_model} \P [X=x,P\in B]=\int _B \P [M_p=x]f_P(p)\,dp \end{equation}

where $x\in \{0,\ldots ,10\}$ and $B\sw \R $. In particular, Lemma 1.7.1 tells us that $X|_{\{P=p\}}\eqd \Bin (10,p)$.

If we wanted to sample $X$, with the random parameter given by $P$, we can use a two-step procedure. First, we sample the value of $p$ according to $P\sim \Beta (2,8)$. Then, we sample $M_p\sim \Bin (10,p)$, using whichever value of $p$ we obtained. The result of this procedure is our model, $X$, for the data. We’ll come back to this example shortly.

We are now ready to set up the set of type of models we are interested in. We will refer to them as Bayesian models, for a reason that will become clear in the next section. They come in two flavours: discrete data and continuous data. We will study the case of discrete data first, in the next section. In this case the model will be a generalized version of (2.2), where we allow any family of discrete random variables in place of $(M_p)$ and any continuous random variable in place of $P$. We will handle the case of continuous data later on, in Chapter 3.