Bayesian Statistics

$\newcommand{\footnotename}{footnote}$ $\def \LWRfootnote {1}$ $\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\let \LWRorighspace \hspace $ $\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }$ $\newcommand {\mathnormal }[1]{{#1}}$ $\newcommand \ensuremath [1]{#1}$ $\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } $ $\newcommand {\setlength }[2]{}$ $\newcommand {\addtolength }[2]{}$ $\newcommand {\setcounter }[2]{}$ $\newcommand {\addtocounter }[2]{}$ $\newcommand {\arabic }[1]{}$ $\newcommand {\number }[1]{}$ $\newcommand {\noalign }[1]{\text {#1}\notag \\}$ $\newcommand {\cline }[1]{}$ $\newcommand {\directlua }[1]{\text {(directlua)}}$ $\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}$ $\newcommand {\protect }{}$ $\def \LWRabsorbnumber #1 {}$ $\def \LWRabsorbquotenumber "#1 {}$ $\newcommand {\LWRabsorboption }[1][]{}$ $\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }$ $\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }$ $\def \mathcode #1={\mathchar }$ $\let \delcode \mathcode $ $\let \delimiter \mathchar $ $\def \oe {\unicode {x0153}}$ $\def \OE {\unicode {x0152}}$ $\def \ae {\unicode {x00E6}}$ $\def \AE {\unicode {x00C6}}$ $\def \aa {\unicode {x00E5}}$ $\def \AA {\unicode {x00C5}}$ $\def \o {\unicode {x00F8}}$ $\def \O {\unicode {x00D8}}$ $\def \l {\unicode {x0142}}$ $\def \L {\unicode {x0141}}$ $\def \ss {\unicode {x00DF}}$ $\def \SS {\unicode {x1E9E}}$ $\def \dag {\unicode {x2020}}$ $\def \ddag {\unicode {x2021}}$ $\def \P {\unicode {x00B6}}$ $\def \copyright {\unicode {x00A9}}$ $\def \pounds {\unicode {x00A3}}$ $\let \LWRref \ref $ $\renewcommand {\ref }{\ifstar \LWRref \LWRref }$ $ \newcommand {\multicolumn }[3]{#3}$ $\require {textcomp}$ $\newcommand {\intertext }[1]{\text {#1}\notag \\}$ $\let \Hat \hat $ $\let \Check \check $ $\let \Tilde \tilde $ $\let \Acute \acute $ $\let \Grave \grave $ $\let \Dot \dot $ $\let \Ddot \ddot $ $\let \Breve \breve $ $\let \Bar \bar $ $\let \Vec \vec $ $\require {colortbl}$ $\let \LWRorigcolumncolor \columncolor $ $\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigrowcolor \rowcolor $ $\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigcellcolor \cellcolor $ $\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }$ $\require {mathtools}$ $\newenvironment {crampedsubarray}[1]{}{}$ $\newcommand {\smashoperator }[2][]{#2\limits }$ $\newcommand {\SwapAboveDisplaySkip }{}$ $\newcommand {\LaTeXunderbrace }[1]{\underbrace {#1}}$ $\newcommand {\LaTeXoverbrace }[1]{\overbrace {#1}}$ $\newcommand {\LWRmultlined }[1][]{\begin {multline*}}$ $\newenvironment {multlined}[1][]{\LWRmultlined }{\end {multline*}}$ $\let \LWRorigshoveleft \shoveleft $ $\renewcommand {\shoveleft }[1][]{\LWRorigshoveleft }$ $\let \LWRorigshoveright \shoveright $ $\renewcommand {\shoveright }[1][]{\LWRorigshoveright }$ $\newcommand {\shortintertext }[1]{\text {#1}\notag \\}$ $\newcommand {\vcentcolon }{\mathrel {\unicode {x2236}}}$ $\renewcommand {\intertext }[2][]{\text {#2}\notag \\}$ $\newenvironment {fleqn}[1][]{}{}$ $\newenvironment {ceqn}{}{}$ $\newenvironment {darray}[2][c]{\begin {array}[#1]{#2}}{\end {array}}$ $\newcommand {\dmulticolumn }[3]{#3}$ $\newcommand {\LWRnrnostar }[1][0.5ex]{\\[#1]}$ $\newcommand {\nr }{\ifstar \LWRnrnostar \LWRnrnostar }$ $\newcommand {\mrel }[1]{\begin {aligned}#1\end {aligned}}$ $\newcommand {\underrel }[2]{\underset {#2}{#1}}$ $\newcommand {\medmath }[1]{#1}$ $\newcommand {\medop }[1]{#1}$ $\newcommand {\medint }[1]{#1}$ $\newcommand {\medintcorr }[1]{#1}$ $\newcommand {\mfrac }[2]{\frac {#1}{#2}}$ $\newcommand {\mbinom }[2]{\binom {#1}{#2}}$ $\newenvironment {mmatrix}{\begin {matrix}}{\end {matrix}}$ $\newcommand {\displaybreak }[1][]{}$ $ \def \offsyl {(\oslash )} \def \msconly {(\Delta )} $ $ \DeclareMathOperator {\var }{var} \DeclareMathOperator {\cov }{cov} \DeclareMathOperator {\Bin }{Bin} \DeclareMathOperator {\Geo }{Geometric} \DeclareMathOperator {\Beta }{Beta} \DeclareMathOperator {\Unif }{Uniform} \DeclareMathOperator {\Gam }{Gamma} \DeclareMathOperator {\Normal }{N} \DeclareMathOperator {\Exp }{Exp} \DeclareMathOperator {\Cauchy }{Cauchy} \DeclareMathOperator {\Bern }{Bernoulli} \DeclareMathOperator {\Poisson }{Poisson} \DeclareMathOperator {\Weibull }{Weibull} \DeclareMathOperator {\IGam }{IGamma} \DeclareMathOperator {\NGam }{NGamma} \DeclareMathOperator {\ChiSquared }{ChiSquared} \DeclareMathOperator {\Pareto }{Pareto} \DeclareMathOperator {\NBin }{NegBin} \DeclareMathOperator {\Studentt }{Student-t} \DeclareMathOperator *{\argmax }{arg\,max} \DeclareMathOperator *{\argmin }{arg\,min} $ \( \def \to {\rightarrow } \def \iff {\Leftrightarrow } \def \ra {\Rightarrow } \def \sw {\subseteq } \def \mc {\mathcal } \def \mb {\mathbb } \def \sc {\setminus } \def \wt {\widetilde } \def \v {\textbf } \def \E {\mb {E}} \def \P {\mb {P}} \def \R {\mb {R}} \def \C {\mb {C}} \def \N {\mb {N}} \def \Q {\mb {Q}} \def \Z {\mb {Z}} \def \B {\mb {B}} \def \~{\sim } \def \-{\,;\,} \def \qed {$\blacksquare $} \CustomizeMathJax {\def \1{\unicode {x1D7D9}}} \def \cadlag {c\`{a}dl\`{a}g} \def \p {\partial } \def \l {\left } \def \r {\right } \def \Om {\Omega } \def \om {\omega } \def \eps {\epsilon } \def \de {\delta } \def \ov {\overline } \def \sr {\stackrel } \def \Lp {\mc {L}^p} \def \Lq {\mc {L}^p} \def \Lone {\mc {L}^1} \def \Ltwo {\mc {L}^2} \def \toae {\sr {\rm a.e.}{\to }} \def \toas {\sr {\rm a.s.}{\to }} \def \top {\sr {\mb {\P }}{\to }} \def \tod {\sr {\rm d}{\to }} \def \toLp {\sr {\Lp }{\to }} \def \toLq {\sr {\Lq }{\to }} \def \eqae {\sr {\rm a.e.}{=}} \def \eqas {\sr {\rm a.s.}{=}} \def \eqd {\sr {\rm d}{=}} \def \approxd {\sr {\rm d}{\approx }} \def \Sa {(S1)\xspace } \def \Sb {(S2)\xspace } \def \Sc {(S3)\xspace } \)

7.5 Exercises on Chapter 7

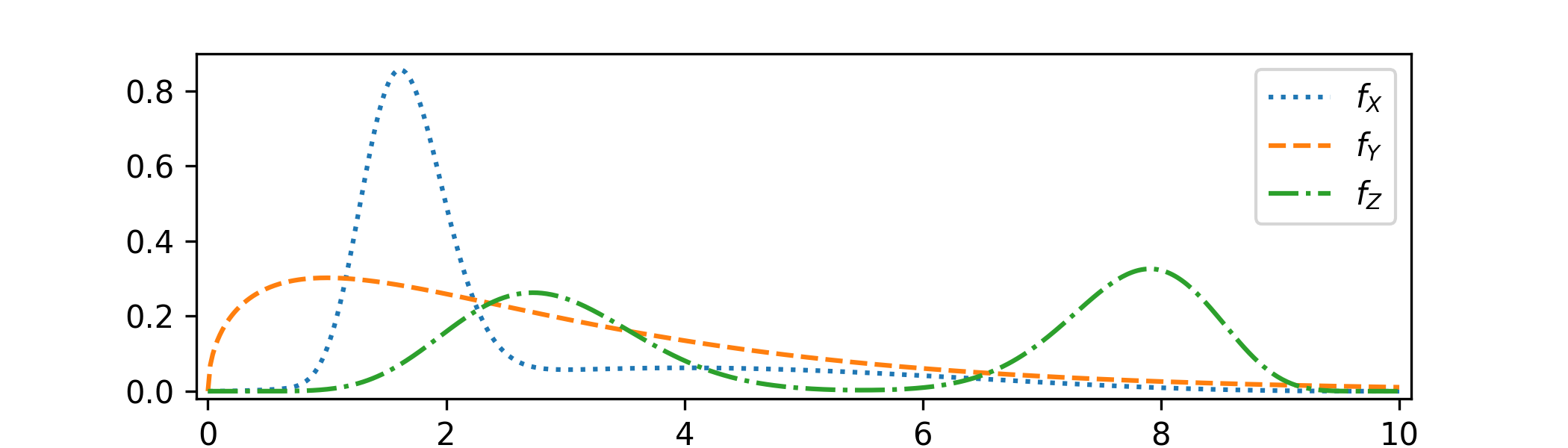
7.1 $\color {blue}\star $ Consider the following sketch of three probability density functions. In each case, discuss whether you think it would reasonable to approximate the distribution with a point estimate. If so, would you prefer the mean, median or mode?
7.2 $\color {blue}\star \,\star $ In the situation of Example 2.3.3, the experiments test the success of a medical treatment. Each trial is expensive, so it is decided by the regulator that further trials of the treatment will be carried out if and only if there is substantial evidence that $\theta >0.2$.
- (a) Using the original prior $\Beta (2,8)$ and the posterior $\Beta (11,19)$ odds obtained after the second round of trials, find the prior and posterior odds ratios of $\theta >0.2$, and find the associated Bayes factor.
- (b) Show that the reference prior for the Binomial distribution is $\Theta \sim \Beta (\frac 12,\frac 12)$ (this generalizes Example 5.3.4).
  
  How much does using this prior change the results of your analysis in (a)?
- (c) Discuss briefly whether the regulator would be interested to see the results in (a), or (b), or both, when making their decision as to whether the trials should proceed further.
7.3 $\color {blue}\star \,\star $ Inside the file 7_earthquakes_japan.csv you will find a dataset listing the number of earthquakes, of magnitude 7.5 or higher, that occurred in Japan during the years 1984-2023. We model the occurrence of earthquakes in a particular year as $\Poisson (\lambda )$, independently for each year, and we consider the hypothesis $H_0:\lambda \geq 2$.
- (a) In Exercise 5.3 we found that the reference prior for the Poisson distribution was
  
  \[f(\lambda )\propto \begin {cases} \lambda ^{-1/2} & \text { for }\lambda >0 \\ 0 & \text { otherwise.} \end {cases} \]
  
  Are the prior odds for $H_0$ defined, with respect to this prior?
- (b) Recall from Exercise 4.3 that the Gamma distribution provides a conjugate prior to the Poisson model family. Using the data given and the weakly informative prior $\lambda \sim \Gam (\frac {5}{4},\frac {1}{5})$, find the posterior distribution for $\lambda $, and find the prior and posterior odds ratios of the evidence in favour of $H_0$ over $H_1$. Calculate the associated Bayes factor and comment on the evidence for $H_0$.
- (c) Repeat part (b) for $H_0:\lambda \geq 3$.
7.4 $\color {blue}\star $ Inside the files 7_hpd_example.ipynb and 7_hpd_example.Rmd you will find code to generate the figure in Exercise 7.2.3. Modify this code (using either file) to construct an equally tailed HPD region $[a,b]$ for the $\ChiSquared (3)$ distribution, such that $\P [\ChiSquared (3)\in [a,b]]=0.7$.
7.5 $\color {blue}\star \,\star $ In this question we model the number of hurricanes per year making landfall in the United States of America using the $\Poisson (\theta )$ distribution. We will assume that each year is independent and we will use a prior $\theta \sim \Exp (\lambda )$.
- (a) Perform an elicitation method of your choice from Section 5.1, either alone or with a parter, to choose the value of $\lambda $ that best expresses your prior beliefs about the number of hurricanes per year that make landfall in the USA.
- (b) Inside the file 7_hurricane_landfalls_usa.csv you will find a dataset corresponding to the years 2015-2022. Use the result of Exercise 4.3 to find the posterior distribution resulting from your prior and this dataset.
  
  Hint: Recall that $\Exp (\lambda )\sim \Gam (1,\lambda )$.
- (c) Sketch an equally tailed $95\%$ HPD region for $\theta $.
7.6 In this question we consider HPD intervals for the mean, using the model $N(\mu ,\phi )^{\otimes n}$ family, with both parameters unknown. We will use the reference prior for this family, which is an improper prior with density function

\[f(\mu ,\phi )= \begin {cases} \frac {1}{\phi } & \text { for }\tau >0\text { and }\mu \in \R \\ 0 & \text { otherwise.} \end {cases}.\]

Write $\bar {x}=\sum _1^n x_i$ and $S^2=\frac {1}{n-1}\sum _1^n (x_i-\bar {x})^2$. It is known that, for this model and reference prior, the variable $t|x=\frac {(\mu |x)-\bar {x}}{S/\sqrt {n}}$ has distribution $t|x\sim \Studentt (n-1)$.
- (a) $\color {blue}\star \,\star $ Inside the file 7_wheat_yields_uk.csv you will find a dataset of the UK wheat yields, measured in tonnes per hectare of farmland, for the years 1983-2022. You may assume that the model $N(\mu ,\phi )^{\otimes 40}$ is appropriate for this data. Construct and sketch an equally tailed $95\%$ HPD region for $t$, and hence give a $95\%$ HPD region for $\mu $.
- (b) $\color {blue}\star \star \star $ Find the posterior density function $f(\mu ,\phi )$, for the model $N(\mu ,\phi )^{\otimes n}$ with the given reference prior. Hence, verify that the distribution of $t|x$ is indeed $\Studentt (n-1)$.
7.7 $\color {blue}\star \star \star $ Prove the continuous case of Lemma 7.1.3. You should use Theorem 3.1.2 along with Exercises 1.8 and 3.6 to justify your calculations.