Bayesian Statistics
3.2 Notation: independent data
We often want to construct a Bayesian model where the data corresponds to \(n\) independent, identically distribution samples from some common distribution. That is, we want our model family to be of the form \(X=(X_1,\ldots ,X_n)\) where the \(X_i\) are independent with the same distribution. It is helpful to have some notation for this.
Given a pair of random variables \(Y\) and \(Z\), we write \(Y\otimes Z\) for the random variable \((Y,Z)\) formed of a copy of \(Y\) and a copy of \(Z\) that are independent of each other. We will tend to use this notation in combination with named distributions. For example, \(X\sim \Normal (0,1)\otimes \Normal (0,1)\) means that \(X=(X_1,X_2)\) is a pair of independent \(\Normal (0,1)\) random variables. When we want to create \(n\) copies we will use a superscript \(\otimes n\), so \(X\sim \Normal (0,1)^{\otimes n}\) means that \(X=(X_1,\ldots ,X_n)\) is a sequence of \(n\) independent \(\Normal (0,1)\) random variables.
Note that if \(X\) has range \(R\) then \(X^{\otimes n}\) has range \(R^n\).
-
Example 3.2.2 Let \(M\) be a continuous random variable with p.d.f. \(f_M\) and let \(X\eqd M^{\otimes n}\). Then \(X\) has p.d.f.
\[f_{X}(x)=\prod _{i=1}^n f_M(x_i),\]
where \(x=(x_1,\ldots ,x_n)\). A similar relationship applies in the case of discrete random variables, to probability mass functions.
-
Example 3.2.3 We are interested to model the duration of time that people spend on social activities. We will use data from the 2015 American Time Use survey, corresponding to the category ‘socializing and communicating with others’.
We decide to model the time spent on a single social activity as an exponential random variable \(\Exp (\lambda )\), where \(\lambda \) is an unknown parameter. This is a common model for time durations. Our data consists of \(n=50\) independent responses, each of which tells us the duration that was spent on a single social activity, in minutes. This gives us the model family
\[M_\lambda =\Exp (\lambda )^{\otimes 50}\]
which has p.d.f.
\(\seteqnumber{0}{3.}{5}\)\begin{align} \label {eq:social_model_pdf} f_{M_\lambda }(x)&=\prod _{i=1}^n \lambda e^{-\lambda x_i} =\lambda ^{50}e^{-\lambda \sum _1^{50}x_i}. \end{align} A single item of data has range \((0,\infty )\) so the range of our model is \((0,\infty )^{50}\).
We need to choose a prior for \(\lambda \). As in Example 2.2.2 we will make a somewhat arbitrary choice, because for now our focus is on understanding how Bayesian updates work. Our prior for the duration of a social activity will be \(\Lambda \sim \Gam (2,60)\),
We can check that this prior sits roughly within the region of parameters that we would expect: it has \(\E [\Lambda ]=\frac {2}{60}=\frac {1}{30}\), which corresponds to an average social activity time of \(30\) minutes, because \(\E [\Exp (\lambda )]=\frac {1}{\lambda }\).
We represent our data as a vector \(x=(x_1,\ldots ,x_{50})\). A histogram of the data is as follows:
It satisfies \(\sum _1^n x_i=6638\), which we can fill into (3.6).
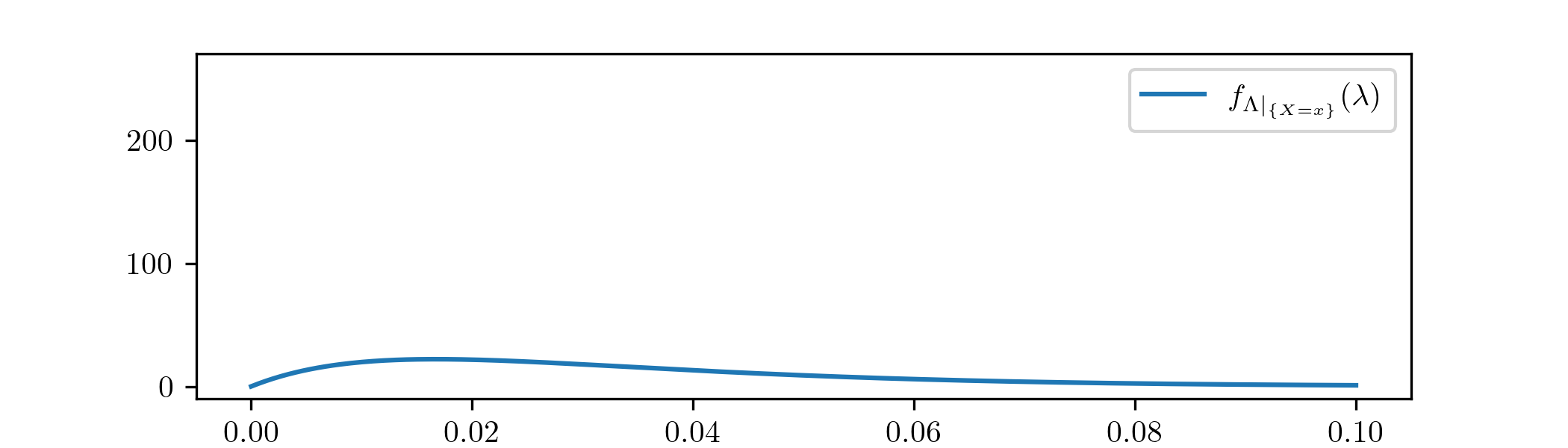
We can find the posterior distribution \(\Lambda |_{\{X=x\}}\) using Theorem 3.1.2. It has p.d.f.
\(\seteqnumber{0}{3.}{6}\)\begin{align} f_{\Lambda |_{\{X=x\}}}(\lambda ) &= \frac {1}{Z}f_{M_\lambda }(x)f_{\Gam (2,60)}(\lambda ) \notag \\ &= \frac {1}{Z}\lambda ^{50}e^{-6638\lambda }\frac {60^2}{\Gamma (2)}\lambda ^{2-1}e^{-60\lambda } \notag \\ &= \frac {1}{Z'}\lambda ^{51}e^{-6698\lambda } \label {eq:social_post_pdf} \end{align} Note that here we have absorbed the factor \(\frac {60^2}{\Gamma (2)}\) into the normalizing constant \(\frac {1}{Z}\) to obtain a new normalizing constant \(\frac {1}{Z'}\). We know that (3.7) is a probability density function, so by Lemma 1.2.5 we have that \(\Lambda |_{\{X=x\}}\sim \Gam (52,6698)\), and we know that \(\frac {1}{Z'}\) must be the normalizing constant of the \(\Gamma (52,6698)\) distribution.
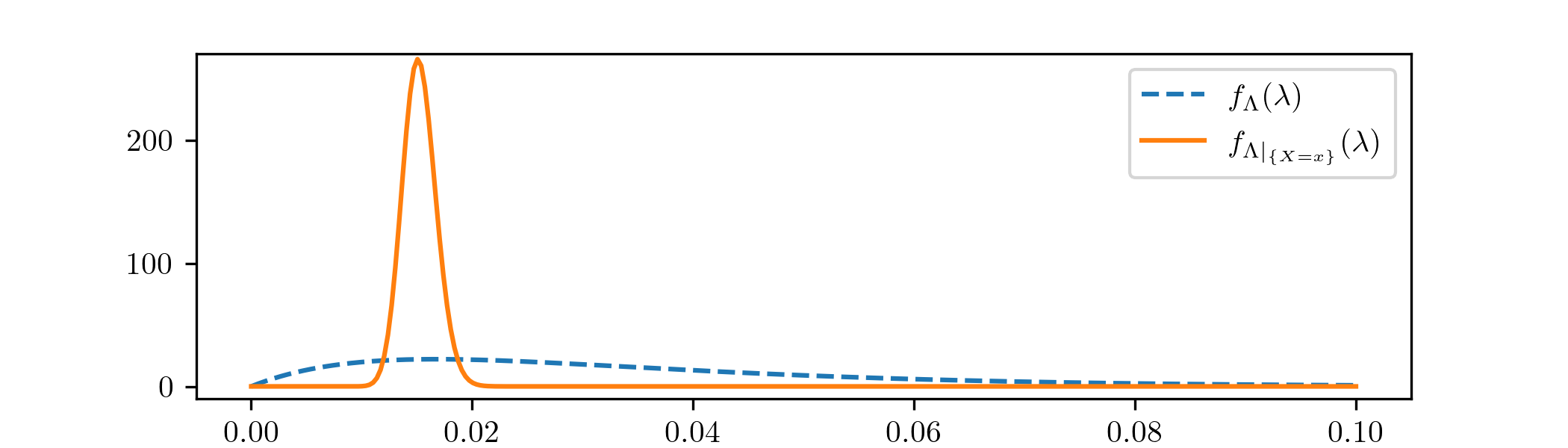
Plotting the prior and posterior probability density functions together gives
Here we see that, even though our prior is spread out across a fairly wide range of values, the posterior has focused very precisely on a small region. By comparison to Example 2.3.3, we have a lot more data here, so our analysis here has produced a higher level of confidence in the best choice of parameter values. Consequently our choice of prior has mattered less than it did in Example 2.3.3.
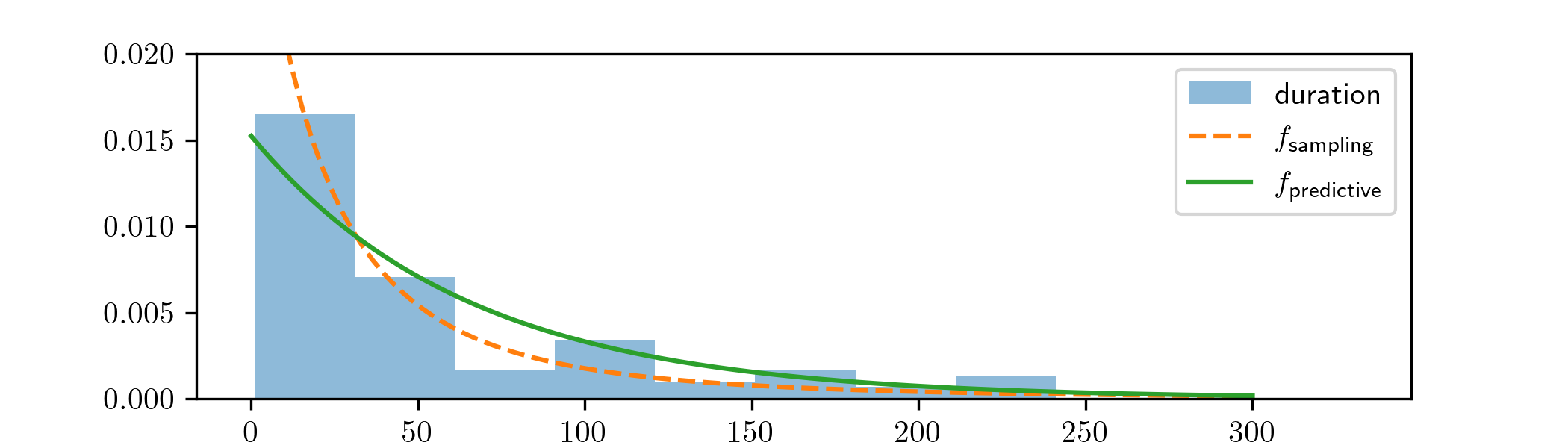
It is sensible to compare the results of our analysis our the histogram of the data \(x\). Our model is for \(50\) independent samples, so technically the sampling and predictive distributions of our model generate \(50\) real-valued samples, which is awkward to sketch. Instead we use the sampling and predictive distributions for a single data point (i.e. the \(n=1\) case of our model). This gives sampling and predictive distributions, from (3.2) and (3.5), with probability density functions
\(\seteqnumber{0}{3.}{7}\)\begin{align*} f_{\text {sampling}}(x_1)&=\int _{\R _d}f_{\Exp (\lambda )}(x_1)f_{\Gamma (2,60)}(\lambda ) \,d\lambda , \\ f_{\text {predictive}}(x_1)&=\int _{\R _d}f_{\Exp (\lambda )}(x'_1)f_{\Gamma (52,6698)}(\lambda ) \,d\lambda . \end{align*} Comparing these to the data, we obtain
It is clear that the predictive distribution is a better match for the data than the sampling distribution. To make the comparison we have scaled the total area of the histogram to be \(1\), to match the fact the area under probability density functions is also \(1\).
-
Remark 3.2.4 In both Chapter 2 and 3 we have used continuous distributions for our random parameters. In principle we could use discrete distributions instead i.e. \(\Pi \) would become a finite set and \(\Theta \) would only be allowed to take values in \(\Pi \). We would need to slightly modify (2.11) and (3.3) for such cases. There aren’t any families of common distributions where the parameters spaces are discrete, and in practice we rarely have a reason to want models of this type. We won’t study models of this type within our course.