Bayesian Statistics
1.4 Conditioning on location
Note that we use \(\eqd \) and not \(=\) in Definition 1.4.2. It is possible to make lots of different random variables \(Y\) that satisfy properties 1 and 2 of Lemma 1.4.1, but they all have the same distribution. Using \(\eqd \) instead of \(=\) captures this fact. We will prove Lemma 1.4.2 shortly, but let us first concentrate on getting the intuition right. Property 1 in Lemma 1.4.1 says that \(Y\) is always inside the set \(A\). Property 2 says that, inside \(A\), \(Y\) behaves like \(X\). (Taking \(B=A\) in property 2 gives property 1, but it will be helpful to refer back to them separately.)
You might like to think of \(Y\) as what happens if the random variable \(X\) is forced to sit inside the set \(A\). It is still (in general) a random quantity, and it reflects exactly the random behaviour of \(X\) inside the set \(A\), but all the behaviour of \(X\) outside of \(A\) is forgotten. Another way to understand \(Y\) is via rejection sampling: we could repeatedly take samples of \(X\) until we obtain a sample of \(X\) that is inside the set \(A\). The random quantity that we obtain from this procedure has precisely the same behaviour as \(Y\).
We will use the usual language of probability to rewrite the event \(\{X\in A\}\) when it is more intuitive to do so. For example, if \(A=[a,b]\) then we might write \(X|_{\{X\in [a,b]\}}\), or if \(A=\{a\}\) then we might write \(X|_{\{X=a\}}\).
-
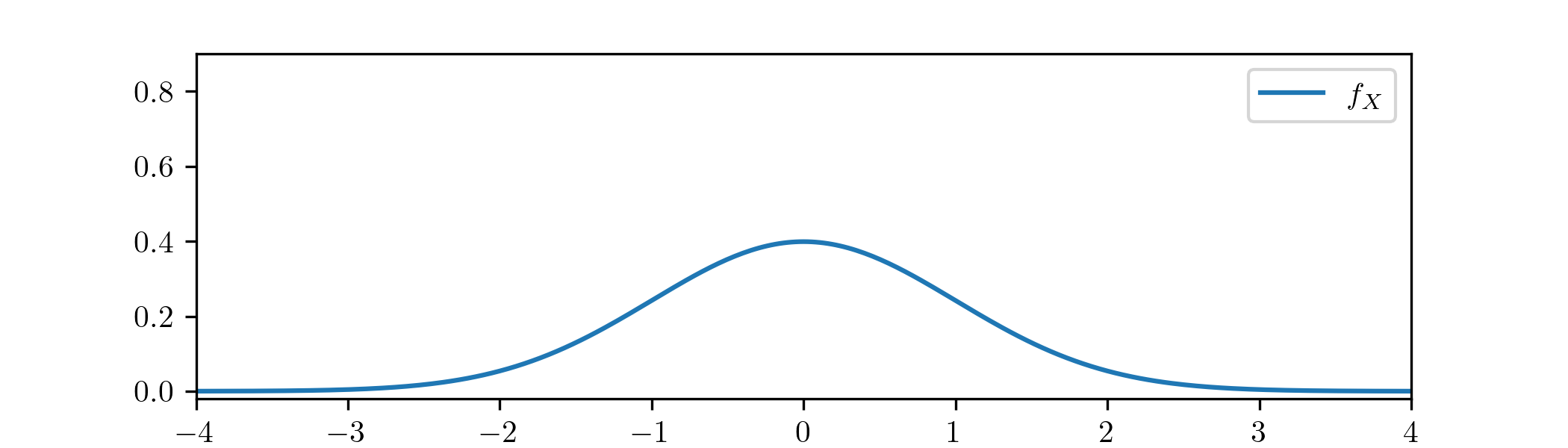
Example 1.4.3 Suppose that \(X\sim \Normal (0,1)\). The values taken by \(X\) are spread out across the real line. The probability density function of \(X\), given by \(f_X(x)=\frac {1}{\sqrt {2\pi }}e^{-x^2/2}\) allows us to visualize the random location of \(X\):
The random variable \(X\) is more likely to be in locations where \(f_X(x)\) takes larger values, or more precisely \(\P [a\leq X\leq b]=\int _a^b f_X(x)\,dx\), the area under the curve \(f_X\) between \(a\) and \(b\).
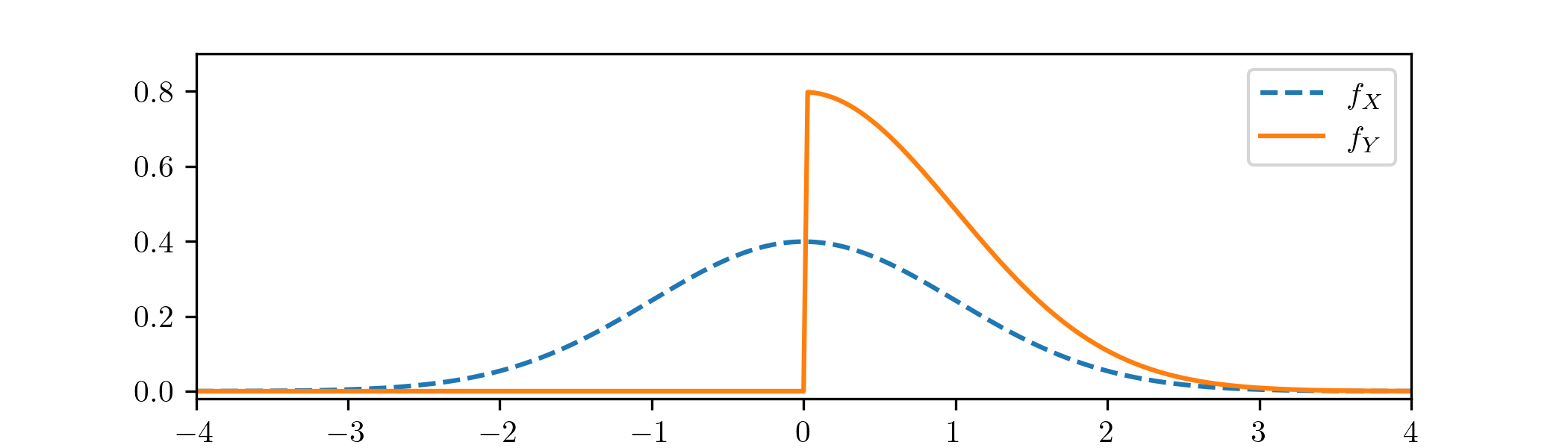
Let \(Y=X|_{\{X\in [0,\infty )\}}\). We can use the properties given in Lemma 1.4.1 to find the distribution of \(Y\), where we take \(A=[0,\infty )\). Firstly, note that property 1 gives \(\P [Y\leq 0]=0\), so \(\P [Y\leq y]=0\) for all \(y\leq 0\). For \(y>0\) we have
\(\seteqnumber{0}{1.}{4}\)\begin{align} \P [Y\leq y] &=\P [Y\leq 0]+\P [0\leq Y\leq y] \notag \\ &= 0 + \frac {\P [0\leq X\leq y]}{\P [0\leq X<\infty ]} \notag \\ &= \frac {\int _0^y f_X(x)\,dx}{1/2} \label {eq:N12} \\ &=\int _0^y 2\frac {1}{\sqrt {2\pi }}e^{-x^2/2}\,dx. \notag \end{align} We therefore obtain that \(Y\) is a continuous random variable with p.d.f.
\(\seteqnumber{0}{1.}{5}\)\begin{equation*} f_Y(y)= \begin{cases} 0 & \text { for }y\leq 0 \\ \sqrt {\frac {2}{\pi }}e^{-y^2/2} & \text { for }y>0. \end {cases} \end{equation*}
Plotting \(f_X\) and \(f_Y\) on the same axis we obtain
Note that \(f_Y(y)\) is zero for \(y\in (-\infty ,0)\), and double the value of \(f_X(y)\) on \(y\in [0,\infty )\). This is not a coincidence. It occurs precisely because \(Y\) retains the ‘same’ randomness as \(X\) inside the set \(A=[0,\infty )\), but \(Y\) can only take values inside the set \(A\), so the p.d.f. within in that segment must be scaled up to ensure that \(\int _\R f_Y(y)\,dy=1\). That fact that this scaling up is by a factor of \(2\), in this example, comes from (1.5) and in particular from \(\P [X\in A]=\frac 12\).
In Problem 1.7 you can explore Example 1.4.3 a bit further, and there is a more general version in Problem 1.8. We will now give a proof of Lemma 1.4.1, based on the idea of rejection sampling that we mentioned below Lemma 1.4.1.
Proof of Lemma 1.4.1: \(\offsyl \) We will discuss this proof in lectures, because Lemma 1.4.1 is fundamental to the whole course and the key ideas of the proof are helpful to understand. The details are less important to us: our focus is on becoming competent practitioners of Bayesian statistics, rather than on becoming able to develop its theory.
Let \(X_1,X_2,\ldots \) be a sequence of i.i.d. copies of the random variable \(X\). Let \(N\in \N \) be the number of the first copy for which \(X_N\in A\). Let us write \(q=\P [X_n\in A]>0\). The events \(\{X_n\in A\}\) are a sequence of independent trials with success probability \(q\), so the number of trials until the first success is \(\Geo (q)\). In particular, since \(\P [\Geo (q)<\infty ]=1\), a success will eventually happen. Let \(N=\min \{n\in \N \-X_n\in A\}\) be the number of trials until this first success.
We claim that \(Y=X_N\) satisfies the two properties required in the statement of the lemma. By definition of \(N\) we have \(\P [X_N\in A]=1\), which shows the first property. To see the second, for \(B\sw A\) we have
\(\seteqnumber{0}{1.}{5}\)\begin{align*} \P [X_N\in B] &= \sum _{n=1}^\infty \P [X_N\in B\text { and }N=n] \\ &= \sum _{n=1}^\infty \P [X_n\in B\text { and }X_{n-1}\notin A, X_{n-2}\notin A,\ldots , X_1\notin A] \\ &= \sum _{n=1}^\infty \P [X_n\in B]\times \P [X_{n-1}\notin A]\times \ldots \times \P [X_1\notin A] \\ &= \sum _{n=1}^\infty \P [X_n\in B](1-q)^{n-1} \\ &= \P [X\in B]\frac {1}{1-q}\sum _{n=1}^\infty (1-q)^{n} \\ &= \P [X\in B]\frac {1}{1-q}\frac {1-q}{q}\\ &= \frac {\P [X\in B]}{\P [X\in A]}. \end{align*} In the above we use independence of the \(X_n\) to deduce the third line. To deduce the fifth line we use that \(X_n\) and \(X\) have the same distribution, hence \(\P [X_n\in B]=\P [X\in B]\), and to deduce the final line we use this same fact with the definition of \(q\). Hence, \(Y=X_N\) satisfies the properties required.
To prove the final part of the lemma, note that if \(Y\) and \(Y'\) both satisfy the two properties then for any \(C\sw \R \) we have
\(\seteqnumber{0}{1.}{5}\)\begin{equation} \label {eq:cond_unique} \P [Y\in C]=\P [Y\in C\cap (\R \sc A)]+\P [Y\in C\cap A]=0+\frac {\P [X\in C\cap A]}{\P [X\in A]} \end{equation}
and the same holds for \(Y'\). To deduce the last equality in (1.6) we have used property 1 for the first term and property 2 for the second term. The right hand side of (1.6) only depends on \(X\), hence \(\P [Y\in C]=\P [Y'\in C]\). Thus \(Y\eqd Y'\). ∎
Proof: We should think of these two cases as (1) conditioning on ‘\(X\) is equal to \(a\)’ and (2) conditioning on ‘\(X\) could be anywhere’. The results of doing so should not be a surprise in either case!
To prove the part 1, if we put \(A=\{a\}\) in Lemma 1.4.1 then the first property gives \(\P [X|_{\{X=a\}}=a]=1\). Therefore \(X|_{\{X=a\}}\) and \(a\) are equal (with probability \(1\)) which means they have the same distribution.
To prove part 2, put \(A=\R ^d\) in Lemma 1.4.1, then the second property gives \(\P [Y\in B]=\frac {\P [X\in B]}{\P [X\in \R ^d]}=\frac {\P [X\in B]}{1}=\P [X\in B]\) for all \(B\sw \R ^d\), which tells us that \(\P [X|_{\R ^d}\in B]=\P [X\in B]\). That is, \(X|_{\R ^d}\) and \(X\) have the same distribution. ∎