Bayesian Statistics

$\newcommand{\footnotename}{footnote}$ $\def \LWRfootnote {1}$ $\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\let \LWRorighspace \hspace $ $\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }$ $\newcommand {\mathnormal }[1]{{#1}}$ $\newcommand \ensuremath [1]{#1}$ $\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } $ $\newcommand {\setlength }[2]{}$ $\newcommand {\addtolength }[2]{}$ $\newcommand {\setcounter }[2]{}$ $\newcommand {\addtocounter }[2]{}$ $\newcommand {\arabic }[1]{}$ $\newcommand {\number }[1]{}$ $\newcommand {\noalign }[1]{\text {#1}\notag \\}$ $\newcommand {\cline }[1]{}$ $\newcommand {\directlua }[1]{\text {(directlua)}}$ $\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}$ $\newcommand {\protect }{}$ $\def \LWRabsorbnumber #1 {}$ $\def \LWRabsorbquotenumber "#1 {}$ $\newcommand {\LWRabsorboption }[1][]{}$ $\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }$ $\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }$ $\def \mathcode #1={\mathchar }$ $\let \delcode \mathcode $ $\let \delimiter \mathchar $ $\def \oe {\unicode {x0153}}$ $\def \OE {\unicode {x0152}}$ $\def \ae {\unicode {x00E6}}$ $\def \AE {\unicode {x00C6}}$ $\def \aa {\unicode {x00E5}}$ $\def \AA {\unicode {x00C5}}$ $\def \o {\unicode {x00F8}}$ $\def \O {\unicode {x00D8}}$ $\def \l {\unicode {x0142}}$ $\def \L {\unicode {x0141}}$ $\def \ss {\unicode {x00DF}}$ $\def \SS {\unicode {x1E9E}}$ $\def \dag {\unicode {x2020}}$ $\def \ddag {\unicode {x2021}}$ $\def \P {\unicode {x00B6}}$ $\def \copyright {\unicode {x00A9}}$ $\def \pounds {\unicode {x00A3}}$ $\let \LWRref \ref $ $\renewcommand {\ref }{\ifstar \LWRref \LWRref }$ $ \newcommand {\multicolumn }[3]{#3}$ $\require {textcomp}$ $\newcommand {\intertext }[1]{\text {#1}\notag \\}$ $\let \Hat \hat $ $\let \Check \check $ $\let \Tilde \tilde $ $\let \Acute \acute $ $\let \Grave \grave $ $\let \Dot \dot $ $\let \Ddot \ddot $ $\let \Breve \breve $ $\let \Bar \bar $ $\let \Vec \vec $ $\require {colortbl}$ $\let \LWRorigcolumncolor \columncolor $ $\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigrowcolor \rowcolor $ $\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigcellcolor \cellcolor $ $\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }$ $\require {mathtools}$ $\newenvironment {crampedsubarray}[1]{}{}$ $\newcommand {\smashoperator }[2][]{#2\limits }$ $\newcommand {\SwapAboveDisplaySkip }{}$ $\newcommand {\LaTeXunderbrace }[1]{\underbrace {#1}}$ $\newcommand {\LaTeXoverbrace }[1]{\overbrace {#1}}$ $\newcommand {\LWRmultlined }[1][]{\begin {multline*}}$ $\newenvironment {multlined}[1][]{\LWRmultlined }{\end {multline*}}$ $\let \LWRorigshoveleft \shoveleft $ $\renewcommand {\shoveleft }[1][]{\LWRorigshoveleft }$ $\let \LWRorigshoveright \shoveright $ $\renewcommand {\shoveright }[1][]{\LWRorigshoveright }$ $\newcommand {\shortintertext }[1]{\text {#1}\notag \\}$ $\newcommand {\vcentcolon }{\mathrel {\unicode {x2236}}}$ $\renewcommand {\intertext }[2][]{\text {#2}\notag \\}$ $\newenvironment {fleqn}[1][]{}{}$ $\newenvironment {ceqn}{}{}$ $\newenvironment {darray}[2][c]{\begin {array}[#1]{#2}}{\end {array}}$ $\newcommand {\dmulticolumn }[3]{#3}$ $\newcommand {\LWRnrnostar }[1][0.5ex]{\\[#1]}$ $\newcommand {\nr }{\ifstar \LWRnrnostar \LWRnrnostar }$ $\newcommand {\mrel }[1]{\begin {aligned}#1\end {aligned}}$ $\newcommand {\underrel }[2]{\underset {#2}{#1}}$ $\newcommand {\medmath }[1]{#1}$ $\newcommand {\medop }[1]{#1}$ $\newcommand {\medint }[1]{#1}$ $\newcommand {\medintcorr }[1]{#1}$ $\newcommand {\mfrac }[2]{\frac {#1}{#2}}$ $\newcommand {\mbinom }[2]{\binom {#1}{#2}}$ $\newenvironment {mmatrix}{\begin {matrix}}{\end {matrix}}$ $\newcommand {\displaybreak }[1][]{}$ $ \def \offsyl {(\oslash )} \def \msconly {(\Delta )} $ $ \DeclareMathOperator {\var }{var} \DeclareMathOperator {\cov }{cov} \DeclareMathOperator {\Bin }{Bin} \DeclareMathOperator {\Geo }{Geometric} \DeclareMathOperator {\Beta }{Beta} \DeclareMathOperator {\Unif }{Uniform} \DeclareMathOperator {\Gam }{Gamma} \DeclareMathOperator {\Normal }{N} \DeclareMathOperator {\Exp }{Exp} \DeclareMathOperator {\Cauchy }{Cauchy} \DeclareMathOperator {\Bern }{Bernoulli} \DeclareMathOperator {\Poisson }{Poisson} \DeclareMathOperator {\Weibull }{Weibull} \DeclareMathOperator {\IGam }{IGamma} \DeclareMathOperator {\NGam }{NGamma} \DeclareMathOperator {\ChiSquared }{ChiSquared} \DeclareMathOperator {\Pareto }{Pareto} \DeclareMathOperator {\NBin }{NegBin} \DeclareMathOperator {\Studentt }{Student-t} \DeclareMathOperator *{\argmax }{arg\,max} \DeclareMathOperator *{\argmin }{arg\,min} $ \( \def \to {\rightarrow } \def \iff {\Leftrightarrow } \def \ra {\Rightarrow } \def \sw {\subseteq } \def \mc {\mathcal } \def \mb {\mathbb } \def \sc {\setminus } \def \wt {\widetilde } \def \v {\textbf } \def \E {\mb {E}} \def \P {\mb {P}} \def \R {\mb {R}} \def \C {\mb {C}} \def \N {\mb {N}} \def \Q {\mb {Q}} \def \Z {\mb {Z}} \def \B {\mb {B}} \def \~{\sim } \def \-{\,;\,} \def \qed {$\blacksquare $} \CustomizeMathJax {\def \1{\unicode {x1D7D9}}} \def \cadlag {c\`{a}dl\`{a}g} \def \p {\partial } \def \l {\left } \def \r {\right } \def \Om {\Omega } \def \om {\omega } \def \eps {\epsilon } \def \de {\delta } \def \ov {\overline } \def \sr {\stackrel } \def \Lp {\mc {L}^p} \def \Lq {\mc {L}^p} \def \Lone {\mc {L}^1} \def \Ltwo {\mc {L}^2} \def \toae {\sr {\rm a.e.}{\to }} \def \toas {\sr {\rm a.s.}{\to }} \def \top {\sr {\mb {\P }}{\to }} \def \tod {\sr {\rm d}{\to }} \def \toLp {\sr {\Lp }{\to }} \def \toLq {\sr {\Lq }{\to }} \def \eqae {\sr {\rm a.e.}{=}} \def \eqas {\sr {\rm a.s.}{=}} \def \eqd {\sr {\rm d}{=}} \def \approxd {\sr {\rm d}{\approx }} \def \Sa {(S1)\xspace } \def \Sb {(S2)\xspace } \def \Sc {(S3)\xspace } \)

2.2 Discrete Bayesian models

We need two ingredients to construct the model:

1. Let $(M_\theta )_{\theta \in \Theta }$ be a family of discrete random variables with range $R\sw \R ^n$ and parameter space $\Pi \sw \R ^d$.
2. Let $f_\Theta :\R ^d\to [0,\infty )$ be a probability density function with range $\Pi $.

The family $(M_\theta )$ is often referred to in textbooks as ‘the’ model, but to avoid confusion we will use the term model family instead. The possible values of $\theta $ for this family are given by the set $\Pi $, known as parameter space of the model. From Definition 1.3.1, all elements $M_\theta $ of the model family have the same range, which we call the range of the model.

The function $f_\Theta $ is known as the prior or more precisely the prior probability density function, for reasons that will be explained shortly. The distribution with p.d.f. $f_\Theta $ is known as the prior distribution. This is the distribution that we use to sample a random parameter from.

Definition 2.2.1 The discrete Bayesian model associated to $(M_\theta )$ and $f_\Theta $ is the random variable $(X,\Theta )\in \R ^n\times \R ^d$ with distribution given by
$\seteqnumber{0}{2.}{2}$
\begin{equation} \label {eq:bayes_discrete_general} \P [X=x,\Theta \in A]=\int _A\P [M_\theta =x]f_\Theta (\theta )\,d\theta . \end{equation}

The random variable $(X,\Theta )$ is neither discrete nor continuous. The $X$ part is discrete, and the $\Theta $ part (as we will see below) is continuous. Equation (2.3) is (1.13) in the special cases of a discrete model family. Let us unpack our notation in (2.3) a bit:

• $\theta \in \Pi $ is a particular choice of parameter;
• $\Theta $ is a random variable with range $\Pi $, the ‘random version’ of the parameter;
• $X$ is the data sampled by the model, and $x$ is a sample of this data.

From Section 1.7 and Lemma 1.7.1 we know that $\Theta $ has p.d.f. $f_\Theta $ and that $X|_{\{\Theta =\theta \}}\sim M_\theta $ whenever $f_\Theta $ is continuous at $\theta $. To find the (marginal) distribution of the data $X$ we set $A=\R ^d$ in (2.3), giving the probability mass function

\begin{equation} \label {eq:bayes_discrete_general_X_pmf} \P [X=x]=\int _{\R ^d}\P [M_\theta =x]f_\Theta (\theta )\,d\theta . \end{equation}

This is known as the sampling distribution of our Bayesian model.

Example 2.2.2 To fit Example 2.1.1 into this notation, take $M_\theta $ to be the Binomial family with $10$ trials, that is $M_p=\Bin (10,p)$ where $p=\theta $ takes values in $\Pi =[0,1]$. The prior chosen in Example 2.1.1 was $P=\Theta \sim \Beta (2,8)$, which takes values in $[0,1]$, and the p.d.f. we wrote down in (2.1). From (2.3) we obtain a discrete Bayesian model $(X,P)$ with distribution given by
$\seteqnumber{0}{2.}{4}$
\begin{align} \P [X=x,P\in A] &=72\binom {10}{x}\int _{A\cap [0,1]} p^x(1-p)^{10-x}p(1-p)^7\,dp \notag \\ &=72\binom {10}{x}\int _{A\cap [0,1]} p^{1+x}(1-p)^{17-x}\,dp. \label {eq:baby_bayes_full} \end{align} Equation (2.5) is precisely (2.2) with the binomial p.m.f. and beta p.d.f. from (2.1) filled in.

Putting $A=\R ^d$ in (2.5) gives the distribution of $X$, also known as the sampling distribution of our model:
$\seteqnumber{0}{2.}{5}$
\begin{equation} \label {eq:baby_bayes_data} \P [X=x]=72\binom {10}{x}\int _0^1 p^{1+x}(1-p)^{17-x}\,dp. \end{equation}

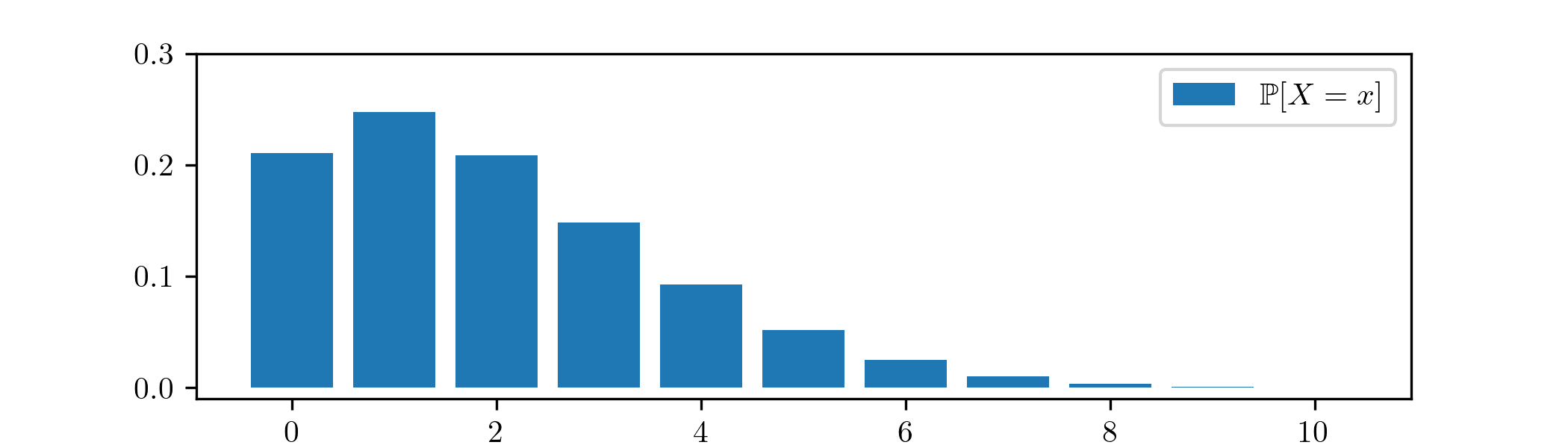
Equations (2.5) and (2.6) are not easy formulae. For the moment we will have to tolerate this sort of thing, before we think of some ways to make our calculations easier in Chapter 4. We can sketch $\P [X=x]$ numerically: