Bayesian Statistics

$\newcommand{\footnotename}{footnote}$ $\def \LWRfootnote {1}$ $\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\let \LWRorighspace \hspace $ $\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }$ $\newcommand {\mathnormal }[1]{{#1}}$ $\newcommand \ensuremath [1]{#1}$ $\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } $ $\newcommand {\setlength }[2]{}$ $\newcommand {\addtolength }[2]{}$ $\newcommand {\setcounter }[2]{}$ $\newcommand {\addtocounter }[2]{}$ $\newcommand {\arabic }[1]{}$ $\newcommand {\number }[1]{}$ $\newcommand {\noalign }[1]{\text {#1}\notag \\}$ $\newcommand {\cline }[1]{}$ $\newcommand {\directlua }[1]{\text {(directlua)}}$ $\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}$ $\newcommand {\protect }{}$ $\def \LWRabsorbnumber #1 {}$ $\def \LWRabsorbquotenumber "#1 {}$ $\newcommand {\LWRabsorboption }[1][]{}$ $\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }$ $\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }$ $\def \mathcode #1={\mathchar }$ $\let \delcode \mathcode $ $\let \delimiter \mathchar $ $\def \oe {\unicode {x0153}}$ $\def \OE {\unicode {x0152}}$ $\def \ae {\unicode {x00E6}}$ $\def \AE {\unicode {x00C6}}$ $\def \aa {\unicode {x00E5}}$ $\def \AA {\unicode {x00C5}}$ $\def \o {\unicode {x00F8}}$ $\def \O {\unicode {x00D8}}$ $\def \l {\unicode {x0142}}$ $\def \L {\unicode {x0141}}$ $\def \ss {\unicode {x00DF}}$ $\def \SS {\unicode {x1E9E}}$ $\def \dag {\unicode {x2020}}$ $\def \ddag {\unicode {x2021}}$ $\def \P {\unicode {x00B6}}$ $\def \copyright {\unicode {x00A9}}$ $\def \pounds {\unicode {x00A3}}$ $\let \LWRref \ref $ $\renewcommand {\ref }{\ifstar \LWRref \LWRref }$ $ \newcommand {\multicolumn }[3]{#3}$ $\require {textcomp}$ $\newcommand {\intertext }[1]{\text {#1}\notag \\}$ $\let \Hat \hat $ $\let \Check \check $ $\let \Tilde \tilde $ $\let \Acute \acute $ $\let \Grave \grave $ $\let \Dot \dot $ $\let \Ddot \ddot $ $\let \Breve \breve $ $\let \Bar \bar $ $\let \Vec \vec $ $\require {colortbl}$ $\let \LWRorigcolumncolor \columncolor $ $\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigrowcolor \rowcolor $ $\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigcellcolor \cellcolor $ $\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }$ $\require {mathtools}$ $\newenvironment {crampedsubarray}[1]{}{}$ $\newcommand {\smashoperator }[2][]{#2\limits }$ $\newcommand {\SwapAboveDisplaySkip }{}$ $\newcommand {\LaTeXunderbrace }[1]{\underbrace {#1}}$ $\newcommand {\LaTeXoverbrace }[1]{\overbrace {#1}}$ $\newcommand {\LWRmultlined }[1][]{\begin {multline*}}$ $\newenvironment {multlined}[1][]{\LWRmultlined }{\end {multline*}}$ $\let \LWRorigshoveleft \shoveleft $ $\renewcommand {\shoveleft }[1][]{\LWRorigshoveleft }$ $\let \LWRorigshoveright \shoveright $ $\renewcommand {\shoveright }[1][]{\LWRorigshoveright }$ $\newcommand {\shortintertext }[1]{\text {#1}\notag \\}$ $\newcommand {\vcentcolon }{\mathrel {\unicode {x2236}}}$ $\renewcommand {\intertext }[2][]{\text {#2}\notag \\}$ $\newenvironment {fleqn}[1][]{}{}$ $\newenvironment {ceqn}{}{}$ $\newenvironment {darray}[2][c]{\begin {array}[#1]{#2}}{\end {array}}$ $\newcommand {\dmulticolumn }[3]{#3}$ $\newcommand {\LWRnrnostar }[1][0.5ex]{\\[#1]}$ $\newcommand {\nr }{\ifstar \LWRnrnostar \LWRnrnostar }$ $\newcommand {\mrel }[1]{\begin {aligned}#1\end {aligned}}$ $\newcommand {\underrel }[2]{\underset {#2}{#1}}$ $\newcommand {\medmath }[1]{#1}$ $\newcommand {\medop }[1]{#1}$ $\newcommand {\medint }[1]{#1}$ $\newcommand {\medintcorr }[1]{#1}$ $\newcommand {\mfrac }[2]{\frac {#1}{#2}}$ $\newcommand {\mbinom }[2]{\binom {#1}{#2}}$ $\newenvironment {mmatrix}{\begin {matrix}}{\end {matrix}}$ $\newcommand {\displaybreak }[1][]{}$ $ \def \offsyl {(\oslash )} \def \msconly {(\Delta )} $ $ \DeclareMathOperator {\var }{var} \DeclareMathOperator {\cov }{cov} \DeclareMathOperator {\Bin }{Bin} \DeclareMathOperator {\Geo }{Geometric} \DeclareMathOperator {\Beta }{Beta} \DeclareMathOperator {\Unif }{Uniform} \DeclareMathOperator {\Gam }{Gamma} \DeclareMathOperator {\Normal }{N} \DeclareMathOperator {\Exp }{Exp} \DeclareMathOperator {\Cauchy }{Cauchy} \DeclareMathOperator {\Bern }{Bernoulli} \DeclareMathOperator {\Poisson }{Poisson} \DeclareMathOperator {\Weibull }{Weibull} \DeclareMathOperator {\IGam }{IGamma} \DeclareMathOperator {\NGam }{NGamma} \DeclareMathOperator {\ChiSquared }{ChiSquared} \DeclareMathOperator {\Pareto }{Pareto} \DeclareMathOperator {\NBin }{NegBin} \DeclareMathOperator {\Studentt }{Student-t} \DeclareMathOperator *{\argmax }{arg\,max} \DeclareMathOperator *{\argmin }{arg\,min} $ \( \def \to {\rightarrow } \def \iff {\Leftrightarrow } \def \ra {\Rightarrow } \def \sw {\subseteq } \def \mc {\mathcal } \def \mb {\mathbb } \def \sc {\setminus } \def \wt {\widetilde } \def \v {\textbf } \def \E {\mb {E}} \def \P {\mb {P}} \def \R {\mb {R}} \def \C {\mb {C}} \def \N {\mb {N}} \def \Q {\mb {Q}} \def \Z {\mb {Z}} \def \B {\mb {B}} \def \~{\sim } \def \-{\,;\,} \def \qed {$\blacksquare $} \CustomizeMathJax {\def \1{\unicode {x1D7D9}}} \def \cadlag {c\`{a}dl\`{a}g} \def \p {\partial } \def \l {\left } \def \r {\right } \def \Om {\Omega } \def \om {\omega } \def \eps {\epsilon } \def \de {\delta } \def \ov {\overline } \def \sr {\stackrel } \def \Lp {\mc {L}^p} \def \Lq {\mc {L}^p} \def \Lone {\mc {L}^1} \def \Ltwo {\mc {L}^2} \def \toae {\sr {\rm a.e.}{\to }} \def \toas {\sr {\rm a.s.}{\to }} \def \top {\sr {\mb {\P }}{\to }} \def \tod {\sr {\rm d}{\to }} \def \toLp {\sr {\Lp }{\to }} \def \toLq {\sr {\Lq }{\to }} \def \eqae {\sr {\rm a.e.}{=}} \def \eqas {\sr {\rm a.s.}{=}} \def \eqd {\sr {\rm d}{=}} \def \approxd {\sr {\rm d}{\approx }} \def \Sa {(S1)\xspace } \def \Sb {(S2)\xspace } \def \Sc {(S3)\xspace } \)

7.2 High posterior density regions

In this section we look at ways to report interval estimates for the unknown parameter $\theta $. The key term used in the Bayesian framework is the following definition.

Definition 7.2.1 A high posterior density region is a subset $\Pi _0\sw \Pi $ that is chosen to minimize the size of $\Pi _0$ and maximize $\P [\Theta |_{\{X=x\}}\in \Pi _0]$.

This is a practical definition rather than a mathematical one: we must choose how to balance the minimization of $\Pi _0$ against maximization of $\P [\Theta |_{\{X=x\}}\in \Pi _0]$ as best we can, and in some situations there is no single right answer. We write HPD region, for short. In some textbooks they are known as HDRs.

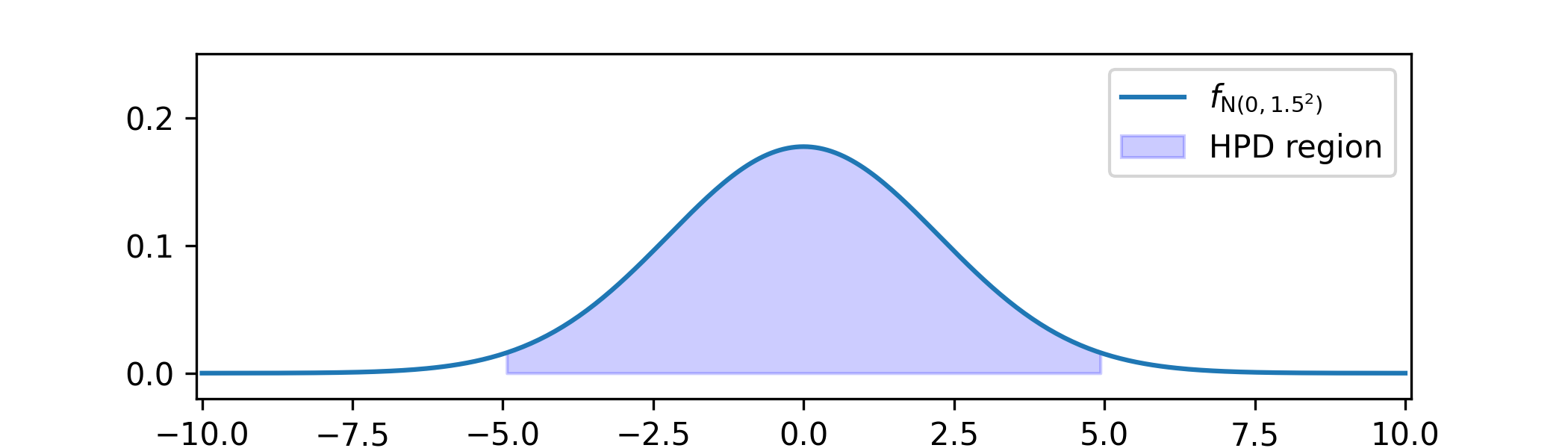
Example 7.2.2 Suppose that our posterior has come out as $\Theta |_{\{X=x\}}\sim \Normal (0,1.5^2)$.

We choose our HPD region to be $[-5,5]$. This region is much smaller than the range of $\Theta $, which is the whole of $\R $. The probability that it contains $\Theta |_{\{X=x\}}$ is given by $\P [-5\leq N(0,1.5^2)\leq 5]=0.97$ to 2 decimal places.

More generally, if we are dealing with a continuous distribution with a single peak then it is common to choose a HPD region of the form $\Pi _0=[a,b]$ where

\begin{equation} \label {eq:hpd_eq_tails_prob} \P \l [\Theta |_{\{X=x\}}<a\r ]=\P \l [\Theta |_{\{X=x\}}>b\r ]=\frac {1-p}{2} \end{equation}

and some value is picked for $p\in (0,1)$. HPD intervals of this type are said to be equally tailed. They always contain the mode of $\Theta |_{\{X=x\}}$, and from (7.3) we have $\P [\Theta |_{\{X=x\}}\in [a,b]]=p$. By symmetry the HPD region in Example 7.2.2 is equally tailed, and we will give an asymmetric case in Example 7.2.3.

A value of $p$ close to $1$ gives a wide interval and a high value for $\P [\Theta |_{\{X=x\}}\in [a,b]]$, whilst a value of $p$ close to $0$ gives a thinner interval but a lower value for $\P [\Theta |_{\{X=x\}}\in [a,b]]$. As in Example 7.2.2, we want to choose $p\in (0,\frac 12)$ to make $[a,b]$ thin and make $\P [\Theta |_{\{X=x\}}\in [a,b]]$ large, if possible.

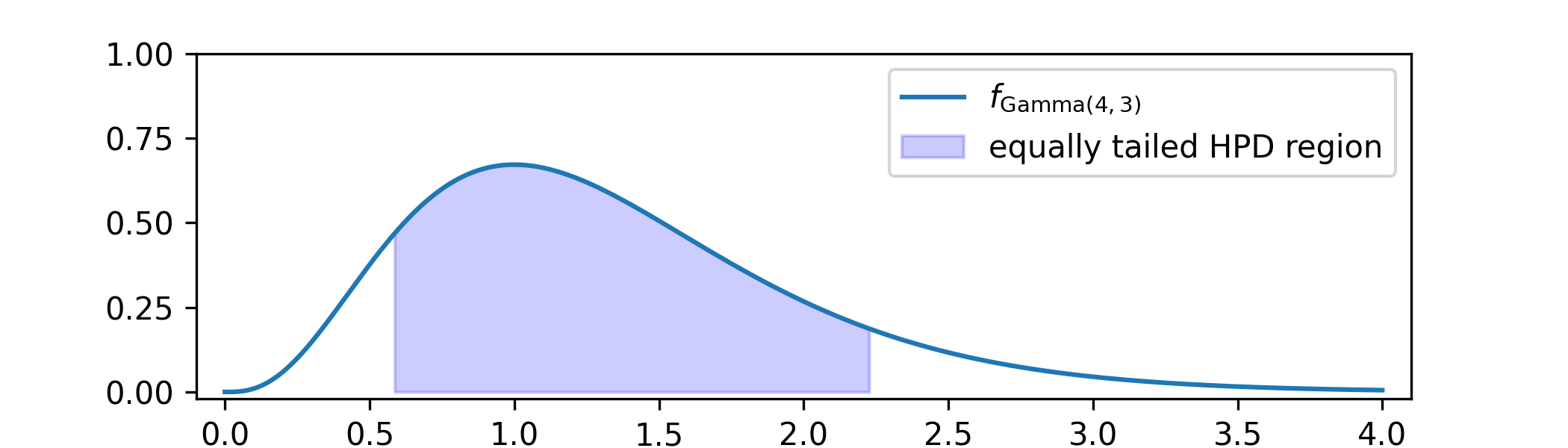
Example 7.2.3 Suppose that our posterior has come out as $\Theta |_{\{X=x\}}\sim \Gamma (3,4)$. We want an equally tailed HPD region $[a,b]$ such that $\P [\Theta |_{\{X=x\}}\in [a,b]]=0.8$.

The region is chosen by finding $a$ such that $\P [\Theta |_{\{X=x\}}<1]=\frac {1-0.8}{2}=0.1$ and $b$ such that $\P [\Theta |_{\{X=x\}}>b]=\frac {1-0.8}{2}=0.1$. These values were found numerically to be $a=0.58$ and $b=2.23$, to two decimal places. You can find the code that generated this example as part of Exercise 7.2.3.

Remark 7.2.4 $\offsyl $ It is possible to construct a form of hypothesis testing based on HPDs. For example, we might by choose an HPD $\Pi _0$ with a $95\%$ probability of containing $\Theta |_{\{X=x\}}$, and then we then reject the hypothesis $\theta =\theta _0$ if and only if $\theta _0\notin \Pi _0$. This approach is known as Lindley’s method.

Remark 7.2.5 $\offsyl $ We can define high prior density regions in the same ways as detailed above, with $\Theta $ in place of $\Theta |_{\{X=x\}}$. These are less useful for parameter estimation although they can be useful for prior elicitation. We implicitly used equally tailed regions of this type in Example 5.1.1, when we asked an elicitee to estimate their 25th and 75th percentiles.