Bayesian Statistics

5.2 Uninformative priors

If we are able to construct a prior distribution based on the opinions of experts, or on earlier research, then it will often be helpful to do so. It is not always possible, particularly if we are dealing with a situation in which very little is known, or if (for whatever reason) we wish to test how well expert opinions agree with the available data. In this section we discuss how to choose a prior that contains little presumption about what the best parameter values are. The general term for such priors is uninformative. Let us detail some approaches based on this idea.

Approach 1: uniform priors. Often, the best trick available here is the most obvious one. If the parameter space \(\Pi \) is a finite interval (for each parameter) then we can simply choose the uniform distribution. This makes our random choice \(\Theta \) of the parameter equally likely to be anywhere within the parameter space \(\Pi \). It is sometimes known as the ‘principle of indifference’, a term introduced by the economist Maynard Keynes in 1921.

There is a distinction to make here between the concepts of ‘no preference’ and ‘equal preference for all outcomes’. We will argue in Section 5.2.1 that the latter perspective is more helpful.

Approach 2: improper priors. If the parameter space is an infinite interval, we cannot choose the uniform distribution, because there is no uniform distribution on an infinite interval! See Exercise 5.6. We need a new definition to understand this situation.

We use the term proper prior density function for the probability density functions of random variables that we could use for the prior. Note that if \(\int _\Pi f(x)\,dx<\infty \) then we can define \(\wt {f}(x)=\frac {1}{\int _\Pi f(y)\,dy} f(x)\) and then \(\wt {f}\) is a proper prior density function with \(f\propto \wt {f}\). Definition 5.2.1 captures the situation that we cannot turn \(f\) into a proper prior by including a normalizing constant. We use the same proper vs. improper terminology for posterior density functions, and for density functions in general.

For example, the functions

\[ g(\theta )=\begin {cases} 1 & \text { for }\theta \in [0,\infty ), \\ 0 & \text { otherwise}, \\ \end {cases} \qquad \text { and } h(\theta )=\begin {cases} \frac {1}{\theta } & \text { for }\theta \in (0,1], \\ 0 & \text { otherwise}, \\ \end {cases} \]

are both improper density functions. You can check that \(\int _\R g(\theta )\,d\theta =\int _\R h(\theta )\,d\theta =\infty \).

When \(\Pi \) is an infinite interval, a common approach is to use an improper prior \(f_\Theta (\theta )\) and use Bayes rule anyway, in which case we obtain

\[f_{\Theta |_{\{X=x\}}}(\theta )\propto L_{M_\theta }(x)f_\Theta (\theta )\]

as usual. There are good theoretical reasons for doing so but they are beyond what we can cover in this course. We will still refer to Theorems 2.4.1 and 3.1.2 for these cases.

If \(\int _\Pi L_{M_\theta }(x)f_\Theta (\theta )\,d\theta \) is finite then we can normalize to obtain \(\wt {f}_{\Theta |_{\{X=x\}}}(\theta )\), which is still a p.d.f. corresponding to some random variable, and we can use that as our posterior. That situation does happen, but it is also possible that \(\int _\Pi L_{M_\theta }(x)f_\Theta (\theta )\,d\theta =\infty \). In this case we could take our improper posterior and use it as another improper prior in a future Bayesian update, and so on – but if we do not eventually reach a proper posterior density function (after some number of Bayesian update steps) then we will find it difficult to interpret the results of our analysis.

Approach 3: use a weak prior. To avoid getting involved with improper priors, a common technique is to choose a weak (but proper) prior distribution that is very well spread out across all plausible regions of the parameter space. We did this in Example 4.2.4, where we took \(\Theta \sim N(30,5^2)\) a normal distribution with a variance so large that it contained very little information about where the value of \(\Theta \approx 30\) would be. A prior with infinite variance, such as the Cauchy distribution, is also an effective way to implement this idea. Note, however, that in many cases choosing a prior with this property will take us outside of the conjugate pairs from Chapter 4, and when that happens we will have to use numerical techniques (to be introduced in Chapter 8) to perform the Bayesian updates.

5.2.1 The philosophy of not knowing anything

Various philosophical arguments have been explored to try and make sense of the idea that a particular choice of prior corresponds to ‘knowing nothing’. For example, consider the following argument:

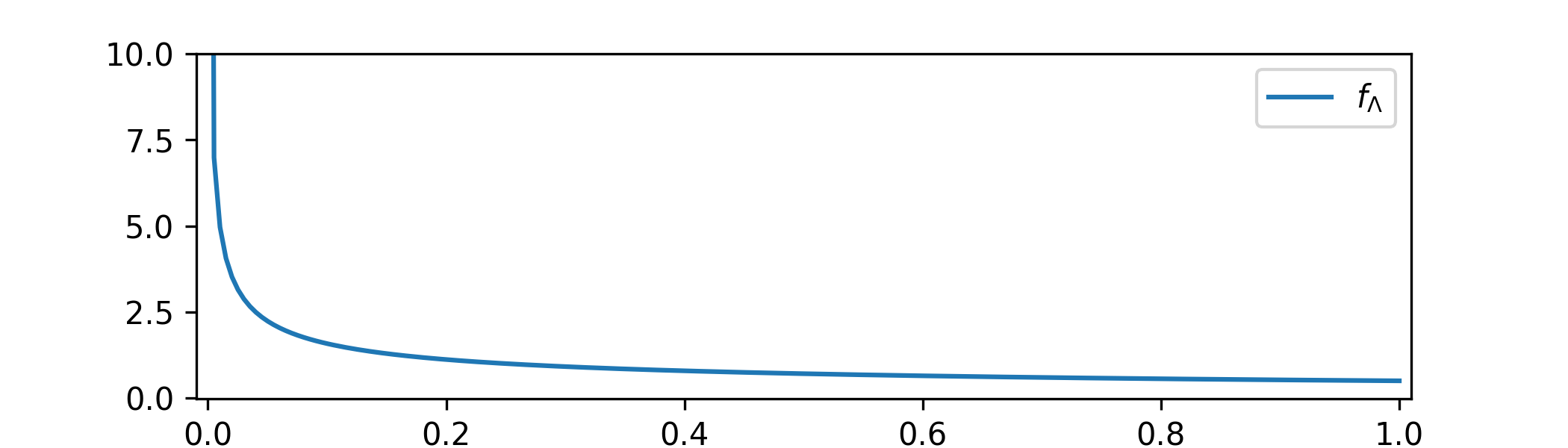
A uniform prior \(\Theta \sim \Unif (0,1)\) supposedly contains no preference for any value of \(\theta \in (0,1)\), but if we use a different parametrization of our model family, say \(\lambda =\theta ^2\) then our prior becomes \(\Lambda =\Theta ^2\) with p.d.f.

\[f_\Lambda (\lambda )=\begin {cases} \frac {1}{2\sqrt {\lambda }} & \text { for }\lambda \in (0,1) \\ 0 & \text { otherwise,} \end {cases}\]

and this is biased towards smaller values in \([0,1]\). If a prior really corresponds to having no preference for any value, then re-parametrization should not change that fact.

This argument is non-mathematical and exploits the fact that its reader has no clear understanding of what ‘no preference’ means. If we consider more aggressive re-parametrizations too, say \(\lambda =\theta ^N\) for large \(N\), then it doesn’t really matter what continuous prior we start with, if \(\Lambda \in [0,1]\) then samples of \(\Lambda =\Theta ^N\) will mostly be very close to zero i.e. nearly deterministic.

What we should take away from this is that Approach 1 and Approach 3 (from Section 5.2) are actually very similar. A slight re-parametrization of our model family will turn one approach into the other, and if we have no strong feeling about which prior is best then we won’t have a strong feeling for which parametrization is best either. This is fine – re-parametrizing our model family slightly won’t change the outcomes of our analysis much either.

I suggest using the (philosophical) viewpoint that the concept of ‘no preference’ does not really exist. The only way to genuinely have no preference about something is to never have thought about it; as soon as you think about it you immediately have a preference, including when that preference is to prefer all outcomes equally.

You will sometimes find that people use ‘no preference’ as a way of disowning (a share of) responsibility for which outcome actually happens. Doing that is a matter of morals and ethics; it will not help us choose an uninformative prior.