In order to perform Bayesian inference computationally, the main requirement is that we can obtain samples from the posterior distribution \(\Theta |_{\{X=x\}}\). We know the p.d.f. from Theorem 2.4.1/3.1.2, but this The most popular strategy
for doing so is based on the Metropolis-Hastings algorithm. We will describe the Metropolis-Hastings algorithm in this section, and explain its application to Bayesian inference in Section 8.3.
8.2.1 The Metropolis-Hastings algorithm
The Metropolis-Hastings algorithm is a general technique for producing samples from a distribution. We will describe it in the case where we take samples of a continuous random variable \(Y\) with
p.d.f. \(f_Y\) and range \(R_Y\sw \R ^d\). The key ingredient of the algorithm is a joint distribution \((Y,Q)\), where \(Q|_{\{Y=y\}}\) and \(Y|_{\{Q=y\}}\) are both well defined for all \(y\in R_Y\),
both with the same range as \(Y\).
Example 8.2.1 Given some continuous
distribution \(Y\) with range \(\R \), a common choice is to take \(Q=Y+\Normal (0,\sigma ^2)\) where \(\sigma >0\) is a constant.
The Metropolis-Hastings algorithm is the following. For now, it won’t be obvious why this algorithm generates samples of \(Y\), but we will address this point soon after. Let \(y_0\) be a point within
\(R_Y\). Then, given \(y_m\) we define \(y_{m+1}\) as follows.
1. Generate a proposal point \(\tilde {y}\) from the distribution of \(Q|_{\{Y=y_m\}}\).
\begin{equation}
\label {eq:mh_update} y_{m+1}=\begin{cases} \tilde {y} & \text { with probability }\alpha , \\ y_m & \text { with probability }1-\alpha . \end {cases}
\end{equation}
The distribution \(Q|_{\{Y=y\}}\) is called the proposal distribution, based on its role in steps 1 and 2. The two cases in step 3 are usually referred to as acceptance (when \(y_{m+1}=\tilde
{y}\)) and rejection (when \(y_{m+1}=y_m\)). The key point is that the algorithm only needs samples from the proposal distribution; we can run it without needing to sample of the distribution of \(Y\)
directly! The Metropolis-Hastings algorithm is useful in cases where the distribution of \(Y\) is unknown or is too complicated to efficiently sample from.
Theorem 8.2.2 Let \((y_m)\) be the random sequence
obtained from the Metropolis-Hastings algorithm. Then for all \(A\sw R_Y\) we have \(\P [y_m\in A]\to \P [Y\in A]\) as \(m\to \infty \).
Theorem 8.2.2 says that if we run the MH algorithm for a long time, so that \(m\) becomes large, the random value of \(y_m\) will have a similar
distribution to \(Y\). We won’t be able to prove Theorem 8.2.2 in this course but we will give a detailed idea of why it is true in Section 8.2.3 (which is off-syllabus). As you might expect, this will involve the precise form of (8.1).
From Lemma 1.6.1 we can rewrite equation (8.1) as \(\alpha =\min \l (1,\frac {f_{Y,Q}(\tilde {y},y_m)}{f_{Y,Q}(y_m,\tilde {y})}\r )\). This is a nicer formula, but the
convention that you will find in all textbooks is to write the form (8.1). The reason for this will become clear in Section
8.2.2.
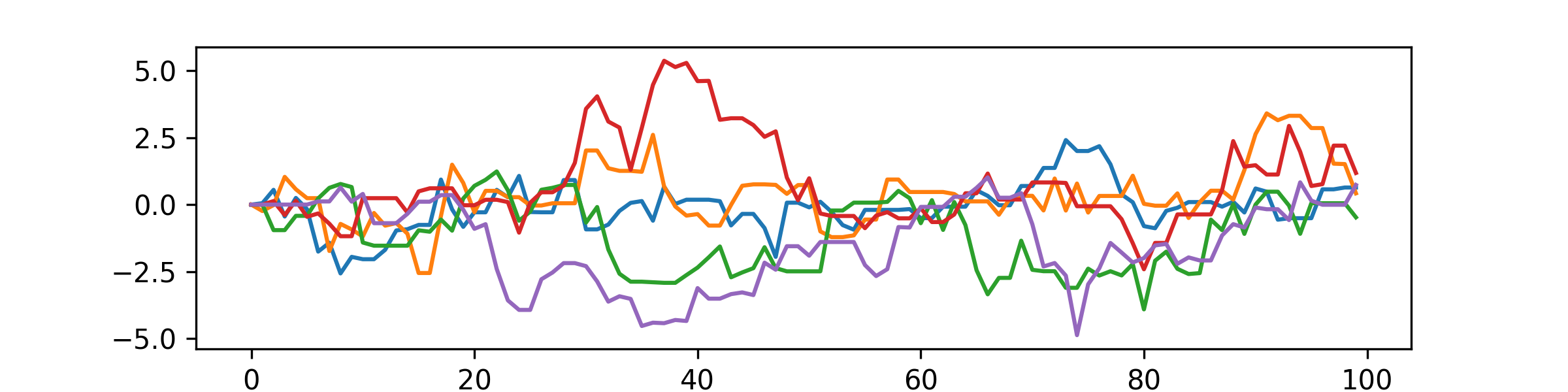
Example 8.2.3 Here’s some examples of the random sequence \((y_m)\)
generated by the MH algorithm, in the case \(Y\sim \Cauchy (0,1)\) with \(Q=Y+\Normal (0,1)\) as in Example 8.2.1.
We’ve shown five sample runs of \((y_m)_{m=1}^{100}\), starting from zero in each case. You can see that sometimes for a few steps of time passes whilst a path does not move – that is when the proposal \(\wt
{y}\) is rejected a few times in a row. When the paths do move, each movement is an (independent) \(\Normal (0,1)\) random variable.
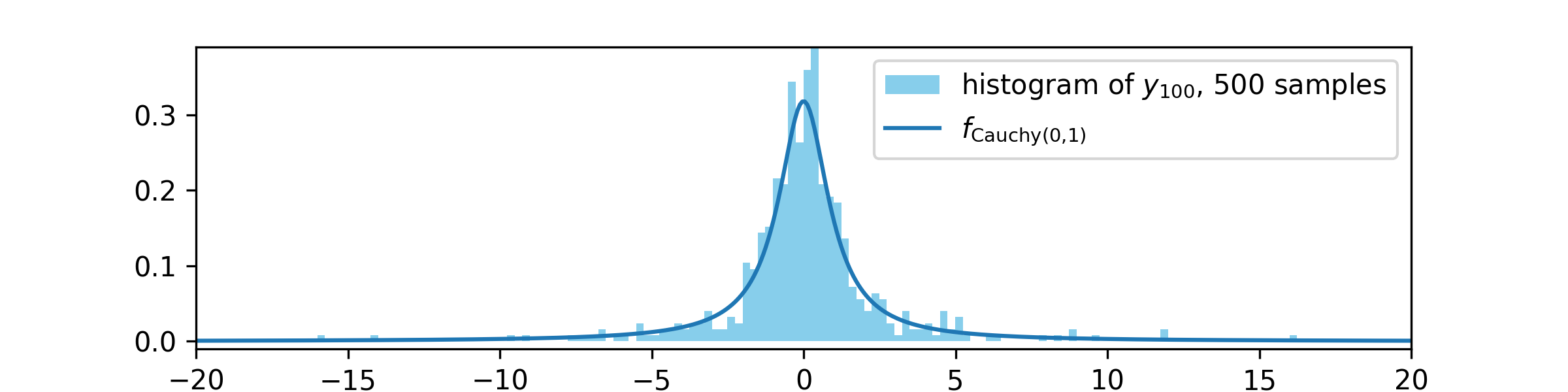
Next we run the MH algorithm \(500\) times, and in each case we record the value of \(y_{100}\). Theorem 8.2.2 tells us that each \(y_{100}\)
should be approximately a sample of \(\Cauchy (0,1)\), so by taking \(500\) samples we should be able to see the shape of the distribution. We plot these values as a histogram and compare to the p.d.f. of
\(\Cauchy (0,1)\), giving
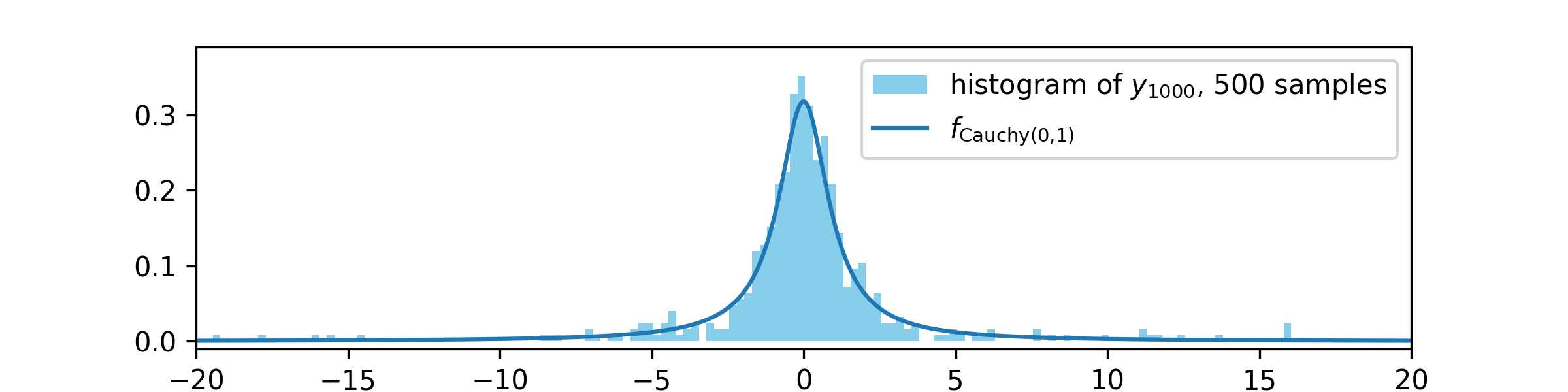
We can see that the histogram is a reasonable match for \(f_{\Cauchy (0,1)}\), so the MH algorithm is behaving as Theorem 8.2.2 predicts. If
we let the MH algorithm have more steps, so that we consider \(y_{1000}\) instead of \(y_{100}\), then we obtain a better approximation:
Of course, we could also obtain a better approximation to the distribution of \(Y\sim \Cauchy (0,1)\) by taking more samples. The code that generated the plots above is given to you for use in several of the
exercises at the end of this chapter.
In statistics you will often hear the terminology ‘\(y_m\) has converged’ used to mean that \(m\) is large enough that \(y_m\) has approximately the same distribution as \(Y\). This is a misuse of terminology, but
it is common and quite helpful in practice. The period before is sometimes known as ‘burn in’.
8.2.2 The Metropolis algorithm
A common technique when using the MH algorithm is to choose \(Q\) in such a way that
for all \(y\) and \(\tilde {y}\). The point of doing so is that it greatly simplifies the formula (8.1) for \(\alpha \),
because the terms on top and bottom involving conditional densities then cancel. The algorithm for updating \(y_n\) then becomes:
1. Generate a candidate point \(\tilde {y}\) from the distribution of \(Q|_{\{Y=y_n\}}\).
More generally, if \(Y\) has range \(\R ^d\) then (8.3) will hold whenever \(Q=Y+Z\) where \(Z\) is a continuous
random variable with a distribution that is symmetric about zero i.e. \(f_Z(z)=f_Z(-z)\). Proving this fact is Exercise ??.
This case is known as the random-walk Metropolis algorithm.
8.2.3 Why does Metropolis-Hastings work? \(\offsyl \)
In order to explain why the MH algorithm for \((Y,Q)\) generates samples of \(Y\), we will need some of the terminology that has been introduced in earlier courses on Markov chains. These courses are
recommended pre-requisites to this course, but they are not compulsory pre-requisites, so this section is off-syllabus. We will sketch out parts of it in lectures, if there is time.
The sequence \((y_m)\) defined by the MH algorithm in Section 8.2.1 is an example of a Markov chain with state space \(R=R_Y\), the range of \(Y\).
In earlier courses you have studied Markov chains with discrete (i.e. finite or countable) state spaces, but in this case the state space is uncountable, because \(Y\) is a continuous random variable. Processes of
this type are known as Markov chains in continuous space.
The key ingredients of a Markov chain with a finite or countable state space are its transition probabilities, which record the probabilities of moving between various states. In continuous space the equivalent
concept is the function
which is known as a transition function for the Markov chain \((X_m)\). It gives the probability of moving to a state within \(A\), from state \(x\), where \(A\sw R\) and \(R\) is the state space of the
chain. You will sometimes see the right hand side of this equation written as \(\P [X_{m+1}\in A|X_m=x]\), with the same meaning.
We say that a continuous random variable \(X\) with p.d.f. \(f_X(x)\) is a stationary distribution for the chain \((X_m)\) if when \(X_m\eqd X\) we have also that \(X_{m+1}\eqd X\). In
symbols, this requirement means that \(\P [X\in A]=\P [X_{m+1}|_{\{X_m=X\}}\in A]\), or equivalently
for all \(A\sw R\). The expression on the right hand side here comes from (8.5), using that \(\P
[X_{m+1}|_{\{X_m=X\}}\in A]=\E [p(X,A)]\).
The definitions of periodicity, irreducibility and the various types of recurrence can be upgraded into continuous space in a natural way. Moreover, there is a convergence theorem for Markov chains in discrete space,
which gives conditions (similar to those for discrete space) for the chain to converge to a unique stationary distribution, as time becomes large. We will not cover these ideas here, but note that our condition in
Section 8.2.1 that \(Q|_{\{Y=y\}}\) is a continuous random variable with range \(R_Y\) means that the sequence \((y_m)\) might jump to anywhere
within \(R_Y\) on any step of time. Under that condition the convergence theorem applies and it is known that the chain \((y_m)\) will converge to a unique stationary distribution. The stationary distribution will
be a continuous random variable and will satisfy (8.6).
We will show here that the transition function given by the MH algorithm satisfies (8.6) with
stationary distribution \(Y\). When this fact is combined with the convergence theorem for continuous space Markov chains, it leads to Theorem 8.2.2 – but we will only cover the calculation of the stationary distribution here. The transition function given by the MH algorithm is
is such that \(\alpha _{y_m,\tilde {y}}\) is precisely (8.1). The MH algorithm will have stationary distribution
\(Y\) if and only if for all \(A\sw R\),
\(\seteqnumber{0}{8.}{8}\)
\begin{align}
\P [Y\in A] &=\int _R p(x,A)f_Y(x)\,dy \label {eq:mh_Y_stationary}
\end{align}
The rest of the argument will concentrate on proving that (8.7) and (8.8) imply that (8.9) holds.
The choice of \(\alpha \) in (8.8) is key. Our next goal is to show that
Remark 8.2.5Recall the heuristic interpretation of probability density functions: \(f_P(p)\)
represents how likely \(P\) is to be close to \(p\). From the MH algorithm, this means that the left hand side of (8.10) represents the likelihood of \(y_{m+1}\approx x\) given that \(y_m\approx y\), where \(y\) is sampled from \(Y\), The right
hand side of (8.10) represents the same concept but with time run in reverse, that is the
likelihood of \(y_{m+1}\approx y\) given that \(y_m\approx x\), where \(x\) is sampled from \(Y\). The choice of \(\alpha _{x,y}\) in (8.8) ensures that these quantities are equal.
Equation (8.10) is closely related to detailed balance equations, which you have seen in earlier
courses for discrete space chains. Loosely, (8.10) gives detailed balance equations for the chain conditional
on the event that a proposal is accepted. The quantity \(\alpha _{x,y}\) controls how likely a proposal for the jump \(x\mapsto y\) is to be accepted, or equivalently how likely the chain is to stand still rather
than move to \(y\). Because \(\alpha _{x,y}\) depends on \(y\), this also controls how likely all of the various possible moves are, which in turn controls the stationary distribution.
\begin{align*}
\int _R p(x,A)f_Y(x)\,dy &=\int _R\int _A \alpha _{x,y}f_{Q|_{\{Y=x\}}}(y)f_Y(x)\,dy\,dx + \int _R\int _R\1_{\{x\in A\}}(1-\alpha _{x,y})f_{Q|_{\{Y=x\}}}f_Y(x)\,dy\,dx \\
&=\int _R\int _A \alpha _{x,y}f_{Y,Q}(x,y)\,dy\,dx + \int _A\int _R(1-\alpha _{x,y})f_{Y,Q}(x,y)\,dy\,dx \\ &=\int _R\int _A \alpha _{y,x}f_{Y,Q}(y,x)\,dy\,dx +\int
_A\int _R f_{Y,Q}(x,y)\,dy\,dx -\int _A\int _R \alpha _{x,y}f_{Y,Q}(x,y)\,dy\,dx \\ &=\int _A\int _R \alpha _{y,x}f_{Y,Q}(y,x)\,dx\,dy +\P [Y\in A, Q\in R] -\int _A\int _R
\alpha _{x,y}f_{Y,Q}(x,y)\,dy\,dx \\ &=\P [Y\in A]
\end{align*}
In the first line of the above we use (8.7) to expand \(p(x,A)\). To obtain the second line we use
Lemma 1.6.1. To obtain the third line we use (8.11) for the first term, and for other terms we simply split the integral into two. In the fourth line we exchange the order of
integration in the first term, and note that the second term can be expressed as a probability. The final line follows because the first and third terms cancel (re-label \(x\) and \(y\) as each other in the first term to
obtain the third) and because \(\P [Q\in R]=1\). We thus obtain (8.9), as required.
Remark 8.2.6It is possible to weaken the conditions on \((Y,Q)\) and allow cases where the
range of \(Q|_{\{Y=y\}}\) is a subset of the range of \(Y\). In this case it becomes necessary that the random sequence \((y_n)\) defined by the algorithm satisfies the condition \(\P [\exists n\in \N ,
y_n\in A]=1\) whenever \(\P [Y\in A]>0\), regardless of the starting point of the chain \((y_n)\). This condition is known as Harris recurrence.
The same algorithm can also produce samples from discrete distributions. In this case we must replace the p.d.f \(f_Y\) by the p.m.f. \(p_Y\), and similarly for the conditional parts in (8.1), but otherwise we proceed exactly as before. We have focused on continuous prior and posterior distributions, with the
consequence that we won’t need the discrete case of Metropolis-Hastings within this course.
