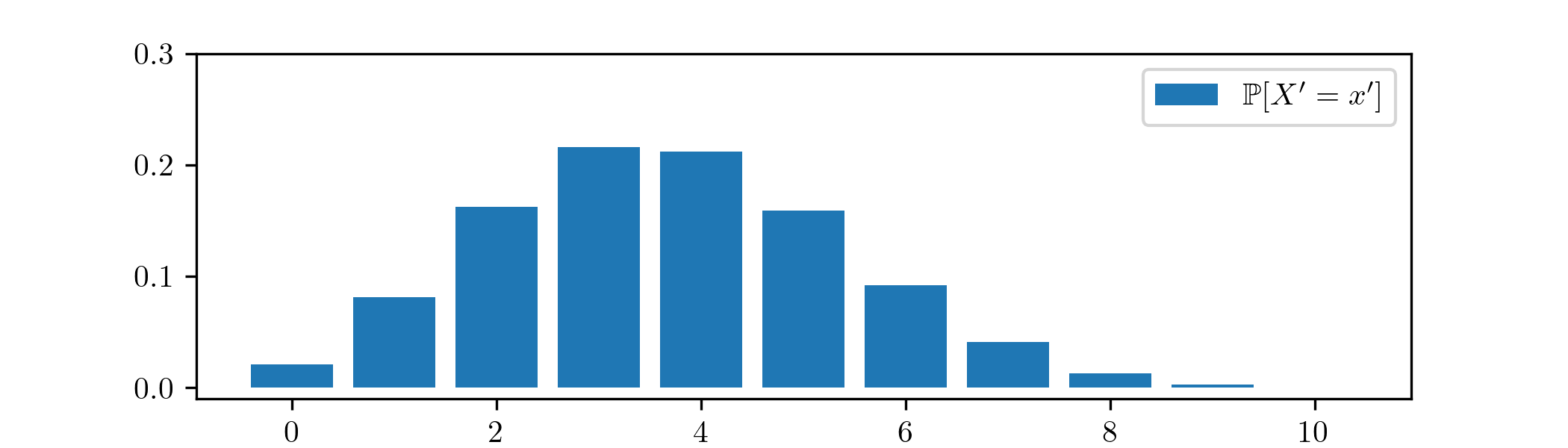Bayesian Statistics
2.3 The posterior distribution
There is one more important piece of terminology associated to \((X,\Theta )\).
It will take a bit of work to understand why \(\Theta |_{\{X=x\}}\) is important. Recall the prior \(\Theta \) is a random variable. The distribution of \(\Theta \), which we usually specify via its p.d.f. \(f_\Theta (\theta )\), is chosen based on our initial beliefs about where the true value of the unknown parameter \(\theta \) might be. We then obtain some data \(x\), coming from reality. The key idea is that \(\Theta |_{\{X=x\}}\) will often be a better choice for the distribution of \(\theta \) than our original choice \(\Theta \) was. This is because \(\Theta |_{\{X=x\}}\) incorporates information from the data that we have. We can summarise this idea as:
\(\seteqnumber{0}{2.}{6}\)\begin{equation} \label {eq:bayes_heuristic} \text {(model parameters)}|_{\{\text {model }=\text { the data we have}\}} =\text {(better model parameters)}. \end{equation}
Here \(|_{\{\ldots \}}\) denotes conditioning. We will use the theory that we developed in Chapter 1 to make sense of (2.7).
The ‘update’ of \(\Theta \) to \(\Theta |_{\{X=x\}}\) is known as a Bayesian update, and the whole process is known as Bayesian learning. The terms ‘prior’ and ‘posterior’ are loose synonyms for ‘before’ and ‘after’, which is why they are used in Bayesian models.
All elements of the discrete family \((M_\theta )\) have the same range \(R\), so \(\P [M_\theta =x]>0\) for all \(x\in R\). It follows that the range of \(\Theta |_{\{X=x\}}\) is the same as the range of \(\Theta \). Checking carefully against the two ingredients at the top of Section 2.2, this means that we can form a new discrete Bayesian model, with the same family \((M_\theta )\), the same parameter space \(\Pi \), the same range \(R\) but with a new prior given by the probability density function \(f_{\Theta |_{\{X=x\}}}\).
With our updated prior, we might want to use our new model to sample data (for whatever purpose). For this we use the sampling p.d.f. (2.4), but now applied to the model with prior \(f_{\Theta |_{\{X=x\}}}\). There is a special piece of terminology for this:
-
Definition 2.3.2 Let \((X,\Theta )\) be a discrete Bayesian model, with parameter space \(\Pi \) and model family \((M_\theta )_{\theta \in \Pi }\). Let \(x\) be an item of data. The predictive distribution is the distribution of \(X'\) where
\(\seteqnumber{0}{2.}{7}\)\begin{equation} \label {eq:bayes_discrete_general_pred_pmf} \P [X'=x']=\int _{\R ^d}\P [M_\theta =x']f_{\Theta |_{\{X=x\}}}(\theta )\,d\theta . \end{equation}
Here, \(X'\) has the same range as \(X\).
-
Example 2.3.3 Let us take the model from Example 2.1.1. We noted in Example 2.2.2 that this model was a discrete Bayesian model. Recall that our model was intended to model the number of successes from a set of 10 independent but identical experiments, where each experiment has an unknown probability \(p\) of success.
The model family we used is \(M_p=\Bin (10,p)\), with only one parameter \(p\), so we take \(\theta =p\). The range of this family is \(R=\{0,1,\ldots ,10\}\). The parameter space is \(\Pi =[0,1]\), and our prior was \(\Theta =P\sim \Beta (2,8)\), which has p.d.f. \(f_P(p)\) that we sketched in Example 2.1.1.
Suppose that we learn that a scientist has carried out the \(10\) experiments, and obtained \(x=4\) successes. We can use Lemma 1.5.1 to compute the posterior \(P|_{\{X=4\}}\), as follows. For \(B\sw \R \),
\(\seteqnumber{0}{2.}{8}\)\begin{align} \P \l [P|_{\{X=4\}}\in B\r ] &=\frac {\P [X=4, P\in B]}{\P [X=4]} \notag \\ &=\frac {72\binom {10}{4}\int _{B\cap [0,1]}p^{1+4}(1-p)^{17-4}\,dp}{72\binom {10}{4}\int _{[0,1]}p^{1+4}(1-p)^{17-4}\,dp} \label {eq:baby_bayes_inf_step}\\ &=\frac {\int _{B\cap [0,1]}p^{5}(1-p)^{13}\,dp}{\mc {B}(6,14)} \notag \\ &=\int _{B\cap [0,1]}\frac {1}{\mc {B}(6,14)}p^{5}(1-p)^{13}\,dp \notag \\ &=\int _B f_{\Beta (6,14)}(p)\,dp \label {eq:baby_bayes_posterior} \end{align} where \(\mc {B}(\alpha ,\beta )=\int _0^1 x^{\alpha -1}(1-x)^{\beta -1}\,dx\) is the Beta function, which gives the normalizing constant of the \(\Beta (\alpha ,\beta )\) distribution. To deduce (2.9) we have used (2.5) for the top and (2.6) for the bottom, with \(x=4\). Note that a factor of \(72\binom {10}{4}\) cancels on the top and bottom.
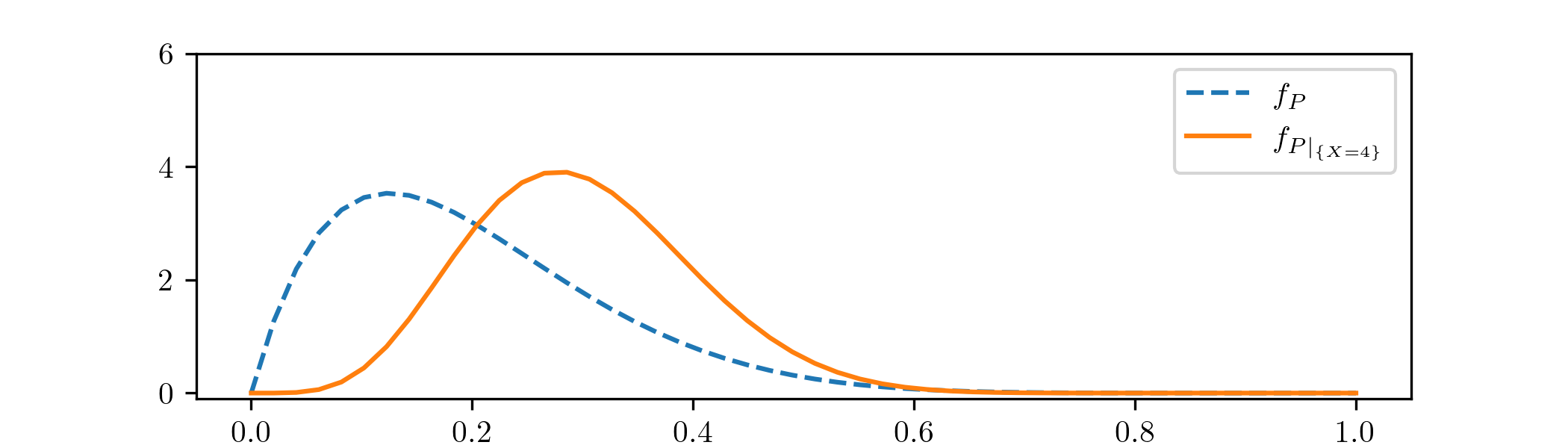
From (2.10) we can recognize \(P|_{\{X=4\}}\sim \Beta (6,14)\) as the posterior distribution of \((X,P)\), given the data \(x=4\). Plotting the density functions of \(P\) and \(P|_{\{X=4\}}\) gives the following:
The effect of incorporating the datapoint \(x=4\) is visible here. Updating our prior p.d.f. \(f_P\) to the posterior p.d.f. \(f_{P|_{\{X=4\}}}\) has resulting in the mass (i.e. the area underneath the curve) moving rightwards, towards the value \(p=0.4\) that corresponds to having \(4/10\) successful experiments. The p.d.f. \(f_{P|_{\{X=4\}}}\) feels both the influence of the prior \(f_P\), as well as the Bayesian update from our data.
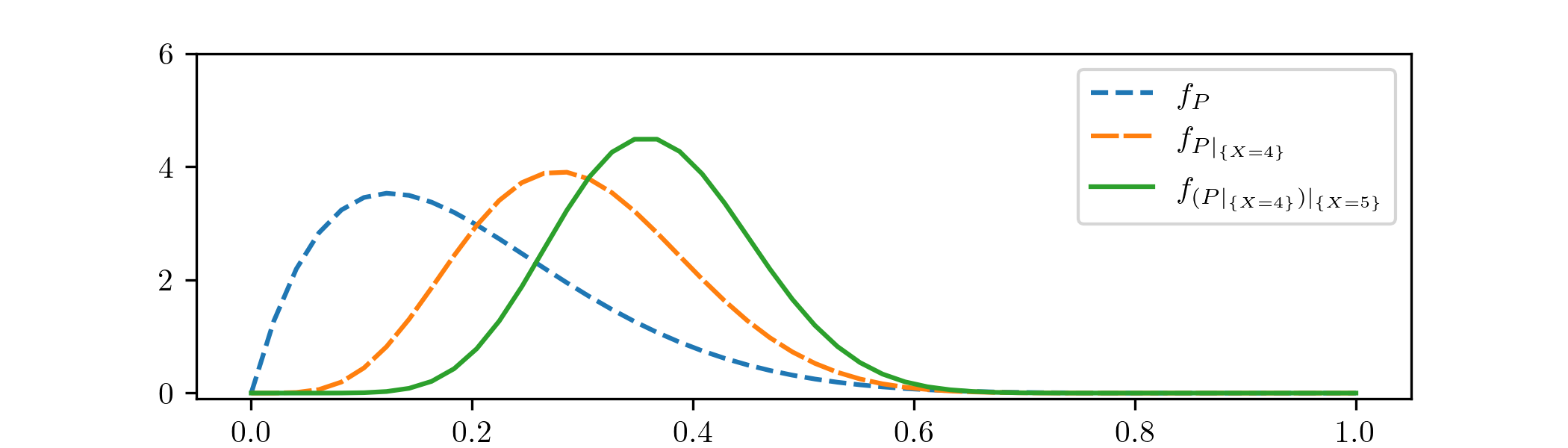
Suppose that we are now given a second piece of data, which is that a second set of \(10\) experiments was done, with \(x=5\) successes. We can use the posterior \(\Beta (6,14)\) that we obtained before as our new prior distribution, to incorporate our improved knowledge about the parameter \(\theta \). We keep the rest of our model as before, and do another Bayesian update to find a new posterior distribution. Going through the same calculations (we’ll omit the details) it turns out that the new posterior is \(\Beta (11,19)\). Including this into our plot we obtain:
We’ve labelled our new posterior as \(f_{(P|_{\{X=4\}})|_{\{X=5\}}}\), to reflect the fact that we’ve done two updates (this is rather lazy notation!). We can see the influence of the new data: our second data point \(x=5\) again corresponds to a higher rate of success than our (updated) model anticipated, which again pulls the mass of the distribution rightwards.
Our model still feels the effect of our initial prior, in the sense that the mean of \(B(11,19)\) is \(11/30\approx 0.37\), which corresponds to a lower success rate than both of our data points. We only have two data points, so it is perhaps best that the initial guess we were given has not been forgotten.
We can also see that the distributions are becoming less spread out with each update. This reflects our models becoming more confident (of the posterior distribution they suggest for \(\theta \)) as we feed them more data. More precisely we can measure the standard deviations becoming smaller: from the reference sheet in Appendix A, \(\Beta (\alpha ,\beta )\) has variance \(\frac {\alpha \beta }{(\alpha +\beta )^2(1+\alpha +\beta )}\), from which the sequence of standard deviations comes out as \(0.12\), \(0.10\) and \(0.087\), each rounded to two significant figures.
Putting our final posterior \(\Beta (11,19)\) back into the same model family, we obtain from (2.8) that the predictive distribution given by our analysis is
\(\seteqnumber{0}{2.}{10}\)\begin{align*} \P [X'=x'] &=\int _0^1 f_{\Bin (10,p)}(x')f_{\Beta (11,19)}(p)\,dp\\ &=\int _0^1\binom {10}{x'}p^{x'}(1-p)^{10-x'}\frac {1}{\mc {B}(11,19)}p^{10}(1-p)^{18}\,dp \\ &=\frac {1}{\mc {B}(11,19)}\binom {10}{x'}\int _0^1 p^{10+x'}(1-p)^{28-x'}\,dp. \end{align*} for \(x'=0,1,\ldots ,10\). Plotting this p.m.f. gives:
We can compare this figure to the sampling p.d.f. in Example 2.2.2, from before we did any Bayesian updates. As we would expect, our estimate of the number of successful experiments now places more weight on larger values.
Calculating the distribution of \(P|_{\{X=4\}}\) in Example 2.3.3 was a bit complicated. For practical purposes we will need to find easier ways of doing Bayesian updates. We’ll do that in Chapter 4, but first we’ll need to finish our development of the theory.
Once you become comfortable with Bayesian updates, it will be tempting to try and compare this new method of statistical inference to things you already know, and to wonder ‘which is better?’. We will think about this in Chapter 6, but there is no simple answer.
In Example 2.3.3 we’ve used several sketches to help us understand the distributions we came across. Exercise 2.1 provides you with template code for doing so yourself. You will find that code useful for several other exercises too.