Bayesian Statistics
4.2 Two more examples of conjugate pairs
There are several examples of conjugate pairs in the exercises at the end of this chapter. We include a couple more here, the first of which generalizes the calculations in Example 3.2.3.
-
Lemma 4.2.1 (Gamma-Exponential conjugate pair) Let \(n\in \N \). Let \((X,\Lambda )\) be a continuous Bayesian model with model family \(M_\lambda \sim \Exp (\lambda )^{\otimes n}\) and parameter \(\lambda \in (0,\infty )\). Suppose that the prior is \(\Lambda \sim \Gam (\alpha ,\beta )\) and let \(x\in (0,\infty )^n\). Then the posterior is \(\Lambda |_{\{X=x\}}\sim \Gam (\alpha +n,\beta +\sum _1^n x_i)\).
Proof: From Theorem 3.1.2 we have that for \(\lambda \in (0,\infty )\)
\(\seteqnumber{0}{4.}{0}\)\begin{align*} f_{\Lambda |_{\{X=x\}}}(\lambda ) &\propto f_{\Exp (\lambda )^{\otimes n}}(x)f_{\Gam (\alpha ,\beta )}(\lambda ) \\ &\propto \l (\prod _{i=1}^n\lambda e^{-\lambda x_i}\r )\l (\frac {\beta ^\alpha }{\Gamma (\alpha )}\lambda ^{\alpha -1}e^{-\beta \lambda }\r ) \\ &\propto \lambda ^n e^{-\lambda \sum _1^n x_i}\lambda ^{\alpha -1}e^{-\beta \lambda }. \\ &\propto \lambda ^{\alpha +n-1}e^{-\lambda (\beta +\sum _1^n x_i)}, \end{align*} By Lemma 1.2.5 we recognize this p.d.f. as \(\Theta |_{\{X=x\}}\sim \Gam (\alpha +n,\beta +\sum _1^n x_i)\). ∎
We’ll now do a more complicated example in which the constant of proportionality would change multiple times – if we were to write it in, which we won’t, thanks to \(\propto \). In Section 4.5 we will look at Bayesian inference for the normal distribution where both \(\mu \) and \(\sigma \) are unknown parameters. For now we view \(\sigma \) as fixed, so the mean \(\mu \) is the only parameter.
-
Lemma 4.2.2 (Normal-Normal conjugate pair) Let \(u\in \R \) and \(\sigma ,s>0\). Let \((X,\Theta )\) be a continuous Bayesian model with model family \(M_{\theta }\sim \Normal (\theta ,\sigma ^2)^{\otimes n}\) and parameter \(\theta \in \R \). Suppose that the prior is \(\Theta \sim \Normal (u,s^2)\) and let \(x\in \R ^n\). Then
\(\seteqnumber{0}{4.}{0}\)\begin{equation} \label {eq:conj_normal_normal} \Theta |_{\{X=x\}}\sim \Normal \l ( \frac {\frac {1}{\sigma ^2}\sum _{1}^n x_i+\frac {u}{s^2}}{\frac {n}{\sigma ^2}+\frac {1}{s^2}}\,,\; \frac {1}{\frac {n}{\sigma ^2}+\frac {1}{s^2}} \r ). \end{equation}
Proof: From Theorem 3.1.2 we have that for \(\theta \in \R \)
\(\seteqnumber{0}{4.}{1}\)\begin{align*} f_{\Theta |_{\{X=x\}}}(\theta ) &\propto f_{\Normal (\theta ,\sigma ^2)^{\otimes n}}(x)f_{\Normal (u,s^2)}(\theta ) \\ &\propto \l (\prod _{i=1}^n\frac {1}{\sqrt {2\pi }}e^{-\frac {(x_i-\theta )^2}{2\sigma ^2}}\r ) \l (\frac {1}{\sqrt {2\pi }}e^{-\frac {(\theta -u)^2}{2s^2}}\r ) \\ &\propto \exp \l (-\frac {1}{2\sigma ^2}\sum _{i=1}^n(x_i-\theta )^2-\frac {1}{2s^2}(\theta -u)^2\r ) \\ &\propto \exp \big (-\mc {Q}(\theta )\big ) \end{align*} where
\(\seteqnumber{0}{4.}{1}\)\begin{equation*} \mc {Q}(\theta ) =\theta ^2\stackrel {A}{\overbrace {\l (\frac {n}{2\sigma ^2}+\frac {1}{2s^2}\r )}} -2\theta \stackrel {B}{\overbrace {\l (\frac {1}{2\sigma ^2}\sum _{i=1}^n x_i+\frac {u}{2s^2}\r )}} +\stackrel {C}{\overbrace {\l (\frac {1}{2\sigma ^2}\sum _{i=1}^n x_i^2+\frac {u^2}{2s^2}\r )}}. \end{equation*}
Completing the square in \(\mc {Q}(\theta )\), using the general form of completing the square (which you can find on the reference sheet in Appendix A), we have that
\(\seteqnumber{0}{4.}{1}\)\begin{align*} f_{\Theta |_{\{X=x\}}}(\theta ) &\propto \exp \l (-A\l (\theta -\frac {B}{A}\r )^2 + C - \frac {B^2}{A}\r ) \\ &\propto \exp \l (-\frac {1}{2(\tfrac {1}{2A})}\l (\theta -\tfrac {B}{A}\r )^2\r ). \end{align*} By Lemma 1.2.5 we recognize this p.d.f. as \(\Theta |_{\{X=x\}}\sim \Normal \l (\frac {B}{A},\frac {1}{2A}\r )\). We have
\[\frac {B}{A}=\frac {\frac {1}{\sigma ^2}\sum _{i=1}^n x_i+\frac {u}{s^2}}{\frac {n}{\sigma ^2}+\frac {1}{s^2}} \qquad \text { and }\qquad \frac {1}{2A}=\frac {1}{\frac {n}{\sigma ^2}+\frac {1}{s^2}},\]
as required. Note that in the first term we have cancelled a factor of \(\frac 12\) from both \(\mc {A}\) and \(\mc {B}\). ∎
From (4.1) we can see that the variance will decrease as \(n\to \infty \), and that for large \(n\) it will be \(\approx \frac {\sigma ^2}{n}\). This agrees with our experience in Example 4.2.4, in which case we had \(\sigma ^2=s^2=0.4^2\), giving variance \(\frac {0.4^2}{n}\). Recall that in our discussion at the end of Example 4.2.4 we noted that the posterior variance had become very small after only \(10\) obserations, despite the prior having a reasonably large variance.
In the formulae we obtained in (4.1) each time a variance appears, for both \(\sigma ^2\) and \(s^2\), it appears on the bottom of a fraction. This suggests that we might obtain nicer formulae if we instead to parameterize the normal distribution as \(\Normal (\mu ,\frac {1}{\tau })\), where by by comparison to our usual parametrization we have written \(\tau =\frac {1}{\sigma ^2}\). It is common to do this in Bayesian statistics and the variable \(\tau \) is then known as precision. We will do this, for example, in Exercise 4.4 which considers the Normal distribution with fixed mean and unknown variance.
You can find a table of conjugate pairs on the reference sheets in Appendix A, below the tables of named distributions. It contains all of the examples within this chapter; there is no need for you to memorize the formulae.
-
Example 4.2.4 Speed cameras are used to measure the speed of individual cars. They do so by recording two images of a moving car, with the second image being captured a fixed time after the first image. By analysing the two images the camera can tell how far the car has travelled in that time, which gives an estimate of its speed. This is not an easy process and there is some degree of error involved.
Suppose that we are trying to assess if the manufacturers description of the error is accurate. The manufacturer claims that, if the true speed is \(30\) (miles per hour) then the speed recorded by the camera can be modelled as a \(\Normal (30,0.16)\) random variable.
We construct an experiment to test this. We set up a camera and drive \(10\) cars past it, each travelling at \(30\) miles per hour (let us assume this can be done accurately, which is not unrealistic using modern cruise control). The camera records speeds of
\(\seteqnumber{0}{4.}{1}\)\begin{equation} \label {eq:camera_data_1} 30.9,\quad 29.9,\quad 30.1,\quad 30.3,\quad 29.7,\quad 30.1,\quad 30.1,\quad 29.2,\quad 30.6,\quad 30.4. \end{equation}
We record this data as \(x=(x_i)_{i=1}^{10}\).
We will come back to this example in future but for now let us assume, for simplicity, that we believe the manufacturers claim that the data will have a normal distribution with variance \(0.16\). We want to see if mean matches up with the figure claimed. We’ll use the model family
\[M_\theta \sim N(\theta ,0.16)^{\otimes 10}\eqd N(\theta ,0.4^2)^{\otimes 10},\]
where the mean \(\theta \) is an unknown parameter. The parameter space of this model is \(\Pi =\R \) and the range of the model is \(\R ^{10}\).
For our prior we will use \(\Theta \sim \Normal (30,5^2)\) which has p.d.f.
\[f_\Theta (\theta )=\frac {1}{5\sqrt {2\pi }}e^{-(x-30)^2/10}.\]
We will study techniques for choosing the prior in Chapter 5. For now our motivation is that we expect the true value for \(\theta \) is about \(30\), but we don’t have a lot of confidence in that, so we pick a fairly large value for the variance.
By Lemma 4.2.2 the posterior distribution is
\[\Theta |_{\{X=x\}}\sim \Normal \l ( \frac {\frac {1}{0.16}\sum _1^{10}x_i+\frac {30}{5^2}}{\frac {10}{0.16}+\frac {1}{5^2}}, \frac {1}{\frac {10}{0.16}+\frac {1}{5^2}} \r ) \eqd \Normal \l (30.13, 0.04^2\r ). \]
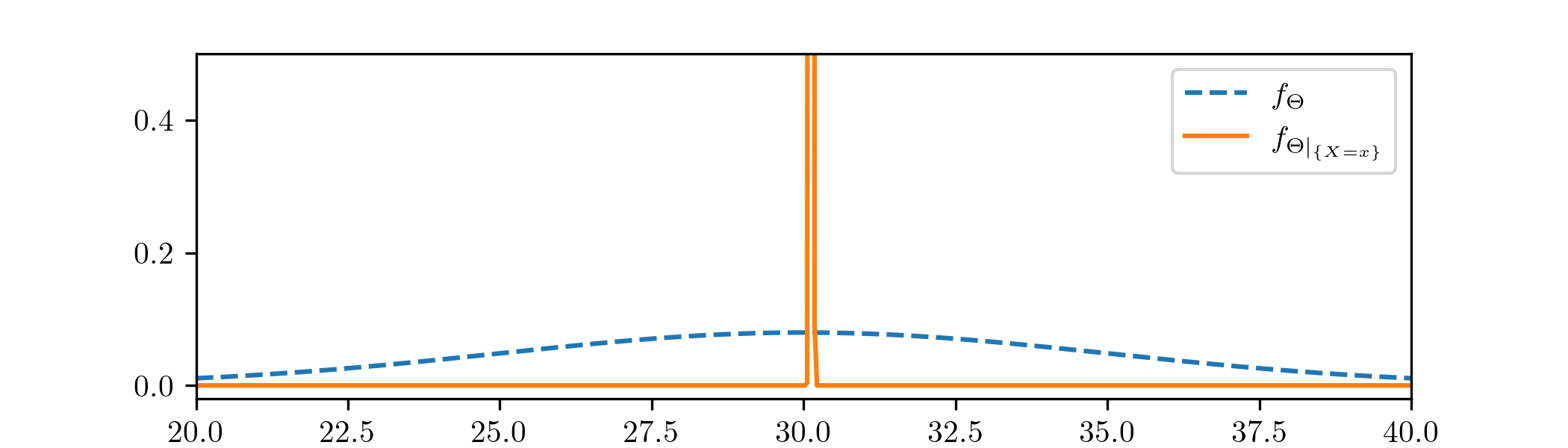
Here we fill in \(\sum _1^{10} x_i=301.4\) and round the parameters to two decimal places. As in our previous examples, let us compare the prior \(\Theta \) to the posterior \(\Theta |_{\{X=x\}}\).
It is difficult to show them on the same axis, so we have had to miss out the top part of the curve \(f_{\Theta |_{\{X=x\}}}\). The outcome is similar to Example 3.2.3, in that the posterior has focused in on a small region. Given our data (4.2) this seems sensible. The influence of the prior has largely been forgotten.
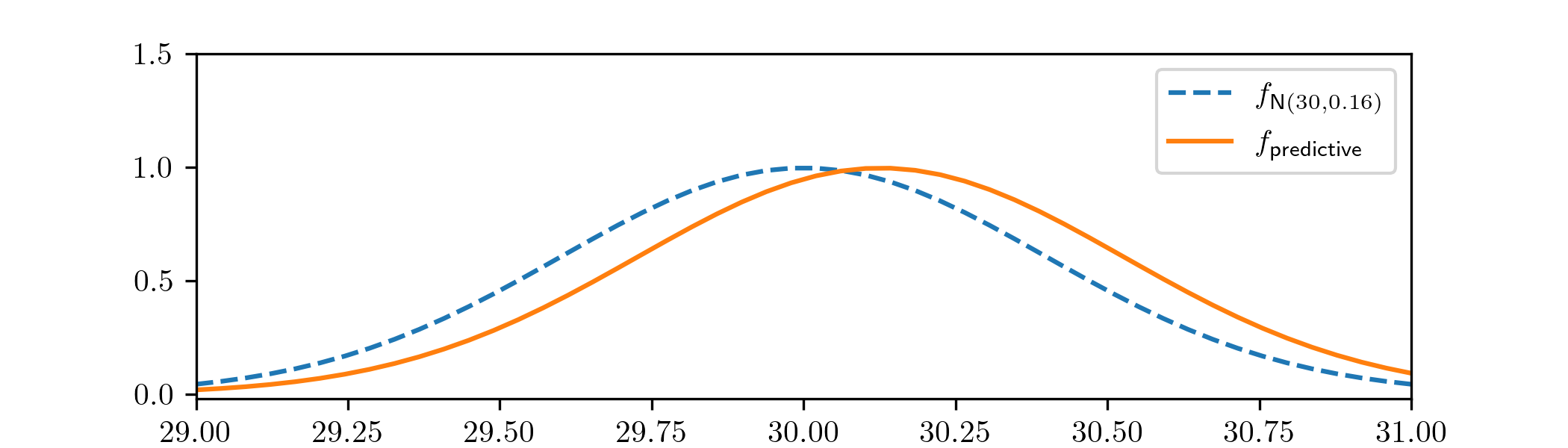
We were originally interested to compare the behaviour the manufacturer claimed that the camera would have, with the results of our experiment. To do so we should compare \(\Normal (30,0.16)\), which is what the manufacturer claimed our experiment should observe, with the predictive distribution from our data analysis. As in Example 3.2.3, what we want here is the predictive distribution for a single data point (i.e. the case \(n=1\)). For that, our model family is \(N(\theta ,0.4^2)\), and our posterior distribution for the unknown parameter \(\theta \) is \(\Normal (\speedcameramean , 0.04^2)\), which gives the p.d.f. of the predictive distribution for a single datapoint as
\(\seteqnumber{0}{4.}{2}\)\begin{align*} f_{\text {predictive}}(x) &=\int _\R f_{\Normal (\theta , 0.4^2)}(x)f_{\Normal (30.13, 0.04^2)}(\theta )\,d\theta \end{align*} which we can evaluate numerically1. We obtain
They are quite similar. If our predictive distribution is a true reflection of the cameras behaviour, it suggests that the camera may be overestimating speeds by a small amount. We would need to do some statistical testing before saying anything more, based on the \(10\) datapoints that we have, and we’ll have to wait until Chapter 7 for that.
We’ll return to this data again in Example 4.5.3, where will also treat the variance as an unknown parameter.