Bayesian Statistics

$\newcommand{\footnotename}{footnote}$ $\def \LWRfootnote {1}$ $\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}$ $\let \LWRorighspace \hspace $ $\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }$ $\newcommand {\mathnormal }[1]{{#1}}$ $\newcommand \ensuremath [1]{#1}$ $\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } $ $\newcommand {\setlength }[2]{}$ $\newcommand {\addtolength }[2]{}$ $\newcommand {\setcounter }[2]{}$ $\newcommand {\addtocounter }[2]{}$ $\newcommand {\arabic }[1]{}$ $\newcommand {\number }[1]{}$ $\newcommand {\noalign }[1]{\text {#1}\notag \\}$ $\newcommand {\cline }[1]{}$ $\newcommand {\directlua }[1]{\text {(directlua)}}$ $\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}$ $\newcommand {\protect }{}$ $\def \LWRabsorbnumber #1 {}$ $\def \LWRabsorbquotenumber "#1 {}$ $\newcommand {\LWRabsorboption }[1][]{}$ $\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }$ $\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }$ $\def \mathcode #1={\mathchar }$ $\let \delcode \mathcode $ $\let \delimiter \mathchar $ $\def \oe {\unicode {x0153}}$ $\def \OE {\unicode {x0152}}$ $\def \ae {\unicode {x00E6}}$ $\def \AE {\unicode {x00C6}}$ $\def \aa {\unicode {x00E5}}$ $\def \AA {\unicode {x00C5}}$ $\def \o {\unicode {x00F8}}$ $\def \O {\unicode {x00D8}}$ $\def \l {\unicode {x0142}}$ $\def \L {\unicode {x0141}}$ $\def \ss {\unicode {x00DF}}$ $\def \SS {\unicode {x1E9E}}$ $\def \dag {\unicode {x2020}}$ $\def \ddag {\unicode {x2021}}$ $\def \P {\unicode {x00B6}}$ $\def \copyright {\unicode {x00A9}}$ $\def \pounds {\unicode {x00A3}}$ $\let \LWRref \ref $ $\renewcommand {\ref }{\ifstar \LWRref \LWRref }$ $ \newcommand {\multicolumn }[3]{#3}$ $\require {textcomp}$ $\newcommand {\intertext }[1]{\text {#1}\notag \\}$ $\let \Hat \hat $ $\let \Check \check $ $\let \Tilde \tilde $ $\let \Acute \acute $ $\let \Grave \grave $ $\let \Dot \dot $ $\let \Ddot \ddot $ $\let \Breve \breve $ $\let \Bar \bar $ $\let \Vec \vec $ $\require {colortbl}$ $\let \LWRorigcolumncolor \columncolor $ $\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigrowcolor \rowcolor $ $\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }$ $\let \LWRorigcellcolor \cellcolor $ $\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }$ $\require {mathtools}$ $\newenvironment {crampedsubarray}[1]{}{}$ $\newcommand {\smashoperator }[2][]{#2\limits }$ $\newcommand {\SwapAboveDisplaySkip }{}$ $\newcommand {\LaTeXunderbrace }[1]{\underbrace {#1}}$ $\newcommand {\LaTeXoverbrace }[1]{\overbrace {#1}}$ $\newcommand {\LWRmultlined }[1][]{\begin {multline*}}$ $\newenvironment {multlined}[1][]{\LWRmultlined }{\end {multline*}}$ $\let \LWRorigshoveleft \shoveleft $ $\renewcommand {\shoveleft }[1][]{\LWRorigshoveleft }$ $\let \LWRorigshoveright \shoveright $ $\renewcommand {\shoveright }[1][]{\LWRorigshoveright }$ $\newcommand {\shortintertext }[1]{\text {#1}\notag \\}$ $\newcommand {\vcentcolon }{\mathrel {\unicode {x2236}}}$ $\renewcommand {\intertext }[2][]{\text {#2}\notag \\}$ $\newenvironment {fleqn}[1][]{}{}$ $\newenvironment {ceqn}{}{}$ $\newenvironment {darray}[2][c]{\begin {array}[#1]{#2}}{\end {array}}$ $\newcommand {\dmulticolumn }[3]{#3}$ $\newcommand {\LWRnrnostar }[1][0.5ex]{\\[#1]}$ $\newcommand {\nr }{\ifstar \LWRnrnostar \LWRnrnostar }$ $\newcommand {\mrel }[1]{\begin {aligned}#1\end {aligned}}$ $\newcommand {\underrel }[2]{\underset {#2}{#1}}$ $\newcommand {\medmath }[1]{#1}$ $\newcommand {\medop }[1]{#1}$ $\newcommand {\medint }[1]{#1}$ $\newcommand {\medintcorr }[1]{#1}$ $\newcommand {\mfrac }[2]{\frac {#1}{#2}}$ $\newcommand {\mbinom }[2]{\binom {#1}{#2}}$ $\newenvironment {mmatrix}{\begin {matrix}}{\end {matrix}}$ $\newcommand {\displaybreak }[1][]{}$ $ \def \offsyl {(\oslash )} \def \msconly {(\Delta )} $ $ \DeclareMathOperator {\var }{var} \DeclareMathOperator {\cov }{cov} \DeclareMathOperator {\Bin }{Bin} \DeclareMathOperator {\Geo }{Geometric} \DeclareMathOperator {\Beta }{Beta} \DeclareMathOperator {\Unif }{Uniform} \DeclareMathOperator {\Gam }{Gamma} \DeclareMathOperator {\Normal }{N} \DeclareMathOperator {\Exp }{Exp} \DeclareMathOperator {\Cauchy }{Cauchy} \DeclareMathOperator {\Bern }{Bernoulli} \DeclareMathOperator {\Poisson }{Poisson} \DeclareMathOperator {\Weibull }{Weibull} \DeclareMathOperator {\IGam }{IGamma} \DeclareMathOperator {\NGam }{NGamma} \DeclareMathOperator {\ChiSquared }{ChiSquared} \DeclareMathOperator {\Pareto }{Pareto} \DeclareMathOperator {\NBin }{NegBin} \DeclareMathOperator {\Studentt }{Student-t} \DeclareMathOperator *{\argmax }{arg\,max} \DeclareMathOperator *{\argmin }{arg\,min} $ \( \def \to {\rightarrow } \def \iff {\Leftrightarrow } \def \ra {\Rightarrow } \def \sw {\subseteq } \def \mc {\mathcal } \def \mb {\mathbb } \def \sc {\setminus } \def \wt {\widetilde } \def \v {\textbf } \def \E {\mb {E}} \def \P {\mb {P}} \def \R {\mb {R}} \def \C {\mb {C}} \def \N {\mb {N}} \def \Q {\mb {Q}} \def \Z {\mb {Z}} \def \B {\mb {B}} \def \~{\sim } \def \-{\,;\,} \def \qed {$\blacksquare $} \CustomizeMathJax {\def \1{\unicode {x1D7D9}}} \def \cadlag {c\`{a}dl\`{a}g} \def \p {\partial } \def \l {\left } \def \r {\right } \def \Om {\Omega } \def \om {\omega } \def \eps {\epsilon } \def \de {\delta } \def \ov {\overline } \def \sr {\stackrel } \def \Lp {\mc {L}^p} \def \Lq {\mc {L}^p} \def \Lone {\mc {L}^1} \def \Ltwo {\mc {L}^2} \def \toae {\sr {\rm a.e.}{\to }} \def \toas {\sr {\rm a.s.}{\to }} \def \top {\sr {\mb {\P }}{\to }} \def \tod {\sr {\rm d}{\to }} \def \toLp {\sr {\Lp }{\to }} \def \toLq {\sr {\Lq }{\to }} \def \eqae {\sr {\rm a.e.}{=}} \def \eqas {\sr {\rm a.s.}{=}} \def \eqd {\sr {\rm d}{=}} \def \approxd {\sr {\rm d}{\approx }} \def \Sa {(S1)\xspace } \def \Sb {(S2)\xspace } \def \Sc {(S3)\xspace } \)

1.8 Exercises on Chapter 1

1.1
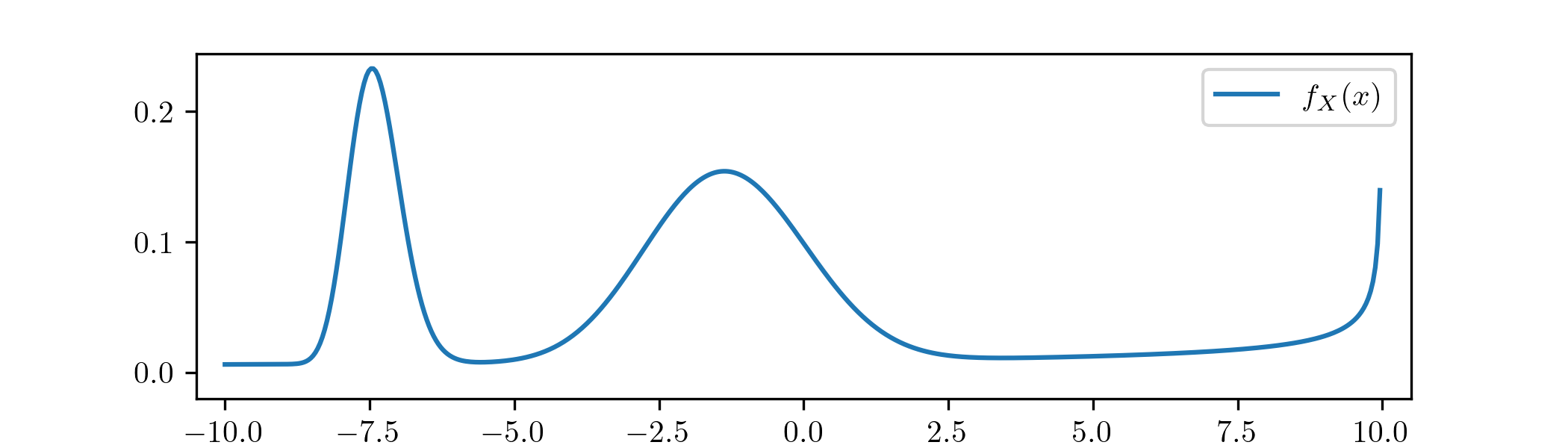
- (a) $\color {blue}\star $ Consider a continuous random variable $X$ with range $R_X=(-10,10)$ and p.d.f. $f_X$ sketched as follows:
  
  In words, explain which parts of $R_X$ are the most likely locations for a random sample of $X$ to be.
- (b) Let $\theta >1$. Check that the function $f:\R \to [0,\infty )$ by $f(x) =\Big \{\begin {smallmatrix} (\theta -1)x^{-\theta } & \text { for } x\geq 1 \hfill \\ 0 & \text { otherwise} \hfill \end {smallmatrix}$ is a probability density function i.e. check that integrating over its range gives $1$.
1.2 $\color {blue}\star $ Let $X\sim \Normal (0,1)$ and let $Y$ be given by $\P [Y=0]=\P [Y=1]=\frac 12$, independently of $Z$. Define a random variable

\[Z=\begin {cases} 0 & \text { if }Y=0, \\ X & \text { if }Y=1. \\ \end {cases} \]

Is $Z$ a discrete random variable, a continuous random variable, or neither?
1.3 $\color {blue}\star \,\star $ Let $a<b<c$, all elements of $\R $. Suppose that $U$ has the continuous uniform distribution on $[a,c]$ and let $U'\eqd U|_{\{U\in [a,b]\}}$.
- (a) Write out the meaning of $U'\eqd U|_{\{U\in [a,b]\}}$, in words.
- (b) Show that $U'$ has the continuous uniform distribution on $[a,b]$.
- (c) Plot the probability density functions of $U$ and $U'$ on the same axis, for the case $a=1,b=2,c=4$.
1.4 $\color {blue}\star \,\star $ Suppose that $G$ has the $\Geo (p)$ distribution, that is $\P [G=g]=p^{g}(1-p)$ for $g\in \{0,1,\ldots \}$, where $p\in [0,1]$. Let $G'\eqd G|_{\{G\geq n\}}$, where $n\in \N $.
- (a) Find the distribution of $G'$.
- (b) Consider the following claim.
  
  Recall that $G$ represents the time of the first failure in a sequence of independent trials, each of which has failure probability $p$. Conditioning $G$ to be greater than or equal to $n$ has the effect of forcing the first $n$ trials to be successful, without changing the distribution of the remaining trials.
  
  Do you agree with this statement? Give brief reasons for your answer.
1.5 $\color {blue}\star $ Let $X\sim \Cauchy (0,1)$ and let $x\in \R $. In the files 1_rejection_sampling.ipynb and 1_rejection_sampling.Rmd you can find a rejection sampling algorithm (as described in our comments below Lemma 1.4.1 or within the proof of that lemma) that obtains samples from $X|_{\{X\geq k\}}$.

Record the time it takes for the code to obtain some samples, for $k=2^n$ for various values of $n\in \{1,2,\ldots \}$. What do you notice? Repeat the experiment with some other distributions.
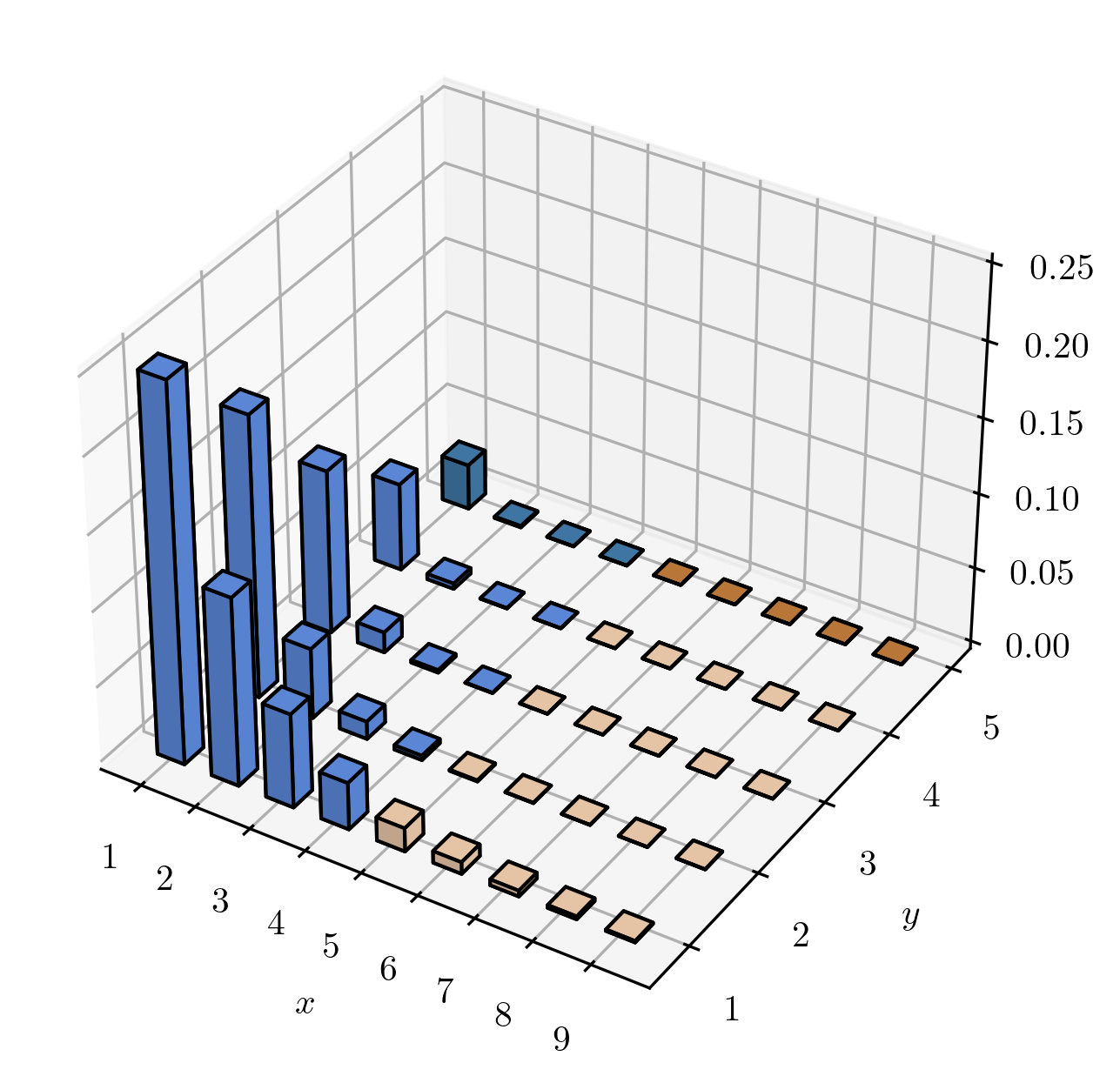
1.6 $\color {blue}\star \,\star $ Let $(X,Y)$ be a discrete random variable with values in $\R ^2$ (so $n=d=1$) with distribution given by
$\seteqnumber{0}{1.}{13}$
\begin{equation} \label {eq:cond_corr_ps} \P [(X,Y)=(x,y)]=\begin{cases} 2^{-xy}(1-2^{-y}) & \text { for }x,y\in \N \\ 0 & \text { otherwise.} \end {cases} \end{equation}

Here is a plot of this function, with shading to indicate regions for which $x\geq 5$ and/or $y=5$.
- (a) Check that the function given in (1.14) is a probability mass function with range $\N ^2$ i.e. check that summing over its range gives $1$. Are $X$ and $Y$ independent?
- (b)
  - (i) Show that for $y\in \N $ we have $\P [Y=y]=\l (\frac 12\r )^y$.
  - (ii) Show that for $x\in \N $ we have $\P [X|_{\{Y=5\}}=x]=\l (1-\frac {1}{2^5}\r )\l (\frac {1}{2^5}\r )^{x-1}.$
  - (iii) Show that for $y\in \N $ we have $\P [Y|_{\{X\geq 5\}}=y]=\l (1-\frac {1}{2^5}\r )\l (\frac {1}{2^5}\r )^{y-1}.$
1.7 $\color {blue}\star \,\star $ Let $X\sim \Normal (0,1)$ and set $A=[0,\infty )$, as in Example 1.4.3. Let $Y'=|X|$. Show that $Y'\eqd X|_{\{X\in A\}}$.
1.8 $\color {blue}\star \star \star $ Let $X$ be a continuous random variable and let $A\sw R_X$ with $\P [X\in A]>0$. Show that $X|_{\{X\in A\}}$ is a continuous random variable with p.d.f.

\[f_{X|_{\{X\in A\}}}(x)= \begin {cases} \frac {f_X(x)}{\P [X\in A]} & \text { if } x\in A \\ 0 & \text {otherwise.} \end {cases} \]
1.9 $\color {blue}\star \star \star $ Prove Lemma 1.2.3.
1.10 $\color {blue}\star \star \star $ Suppose that $X$ and $Y$ are independent random variables, and that $\P [X\in A]>0$. Show that $Y\eqd Y|_{\{X\in A\}}$.